Problem B. 4106. (September 2008)
B. 4106. Determine those quadrilaterals ABCD, such that PA2+PC2=PB2+PD2 for all points P of the plane.
(4 pont)
Deadline expired on October 15, 2008.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Vezessük be az AB=a, BC=b, CD=c, DA=d, AC=e, BD=f jelöléseket. Ha a P pontot A-nak választjuk, akkor az e2=a2+d2 összefüggésre jutunk. Hasonlóképpen kapjuk az e2=b2+c2, a2+b2=f2 és d2+c2=f2 összefüggéseket a P=C, P=B, illetve P=D választással. Az első két összefüggés alapján a2-b2=c2-d2, a másik kettőből pedig a2+b2=c2+d2 következik. Mivel tetszőleges p,q esetén az x-y=p, x+y=q egyenletrendszer egyértelműen megoldható, innen a2=c2 és b2=d2 adódik, vagyis a=c, b=d. Az ABCD négyszög tehát paralelogramma kell legyen. Sőt, e2=b2+c2=b2+a2=f2 miatt e=f, vagyis a feltételek teljesülése esetén az ABCD négyszög csakis téglalap lehet.
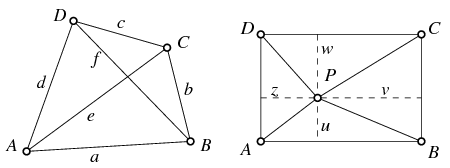
A téglalapokra viszont minden P pont esetén teljesül a feltétel. Ha ugyanis a P pont távolságát az AB, BC, CD, DA egyenesektől rendre u,v,w és z jelöli, akkor a Pithagorasz tétel alapján
PA2+PC2=(u2+z2)+(v2+w2)=(u2+v2)+(w2+z2)=PB2+PD2.
Statistics:
123 students sent a solution. 4 points: 69 students. 3 points: 15 students. 2 points: 4 students. 1 point: 17 students. 0 point: 16 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, September 2008