Problem B. 4110. (September 2008)

B. 4110. The hexagon ABCDEF and the triangle PQR lie in the same plane. The quadrilaterals ABRQ, CDPR, EFQP are all rectangles.

a) Prove that the perpendicular bisectors of the sides BC, DE, FA are concurrent.

b) Show that there exists a triangle P'Q'R', too, for which the quadrilaterals BCR'Q', DEP'R', FAQ'P' are rectangles.

(5 pont)

Deadline expired on October 15, 2008.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás: Tegyük fel, hogy a (2) állítást már igazoltuk. Ekkor a BC, DE, FA oldalak felezőmerőlegesei megegyeznek az R'Q', P'R', Q'P' szakaszok felezőmerőlegeseivel, melyek nyilván a P'Q'R' háromszög köré írható kör középpontjában metszik egymást, igazolva az (1) állítást. A (2) állítás igazolásához először a következő önmagában is érdekes segédtételt bizonyítjuk.

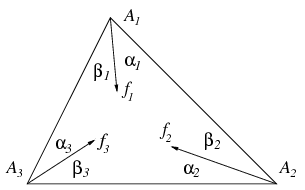
Az A₁A₂A₃ háromszög A_i csúcsából a háromszög belsejében induló f_i félegyenes zárjon be a háromszög megfelelő oldalaival $\alpha$ _i, illetve $\beta$ _i szöget az ábrán látható módon. Az f₁,f₂,f₃ félegyenesek pontosan akkor mennek át egy ponton, ha

sin $\alpha$ ₁sin $\alpha$ ₂sin $\alpha$ ₃=sin $\beta$ ₁sin $\beta$ ₂sin $\beta$ ₃.

Valóban, ha a félegyenesek a P pontban metszik egymást, mely nyilván a háromszög belsejében fekszik, akkor a szinusz-tétel alapján

$\frac{\sin\alpha_1}{\sin\beta_2}\cdot\frac{\sin\alpha_2}{\sin\beta_3}\cdot \frac{\sin\alpha_3}{\sin\beta_1}=\frac{PA_2}{PA_1}\cdot \frac{PA_3}{PA_2}\cdot\frac{PA_1}{PA_3}=1.$

Megfordítva, tegyük fel, hogy sin $\alpha$ ₁sin $\alpha$ ₂sin $\alpha$ ₃=sin $\beta$ ₁sin $\beta$ ₂sin $\beta$ ₃, és a háromszögnek az A₁ csúcsnál lévő szöge hegyesszög. Jelölje P az f₂ és f₃ félegyenesek metszéspontját, mely nyilván a háromszög belsejébe esik, az A₁P félegyenesnek a megfelelő oldalakkal bezárt szögét pedig $\alpha$ ₁', illetve $\beta$ ₁'. A feltételt egybevetve a segédtétel már igazolt felével kapjuk, hogy sin $\alpha$ ₁'/sin $\beta$ ₁'=sin $\alpha$ ₁/sin $\beta$ ₁. Mivel 0<x< $\alpha$ <90^o esetén az f(x)=sin x/sin ( $\alpha$ -x) függvény szigorúan monoton nő, ebből $\alpha$ ₁'= $\alpha$ ₁ adódik, ami azt jelenti, hogy az f₁ félegyenes is áthalad a P ponton.

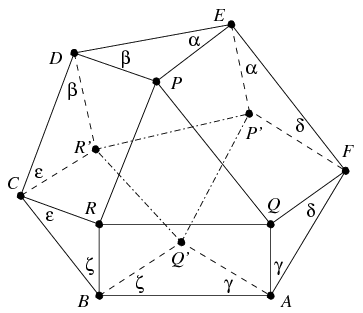
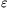A fenti segédtétel felhasználásával a (2) állítás már könnyen levezethető. Párhuzamos eltolással vigyük a BRC, illetve AQF háromszögeket olyan helyzetbe, hogy a C pont D-be, az F pont pedig E-be kerüljön. Ekkor az R és a Q pont is P-be kerül, minek folytán a B és A pontok ugyanazon G pontba kerülnek. A DEG háromszögre alkalmazva a segédtételt kapjuk, hogy sin $\alpha$ sin $\gamma$ sin $\varepsilon$ =sin $\beta$ sin $\delta$ sin $\zeta$ . 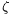Most alkalmazzunk párhuzamos eltolásokat az AB, CD, illetve EF szakaszokra olyan módon, hogy D és E ugyanazon X, F és A ugyanozon Y, B és C pedig ugyanazon Z pontba kerüljenek. 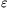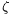Az XYZ háromszögben vegyük fel az X-ből kiinduló f, az Y-ból kiinduló g és a Z-ből kiinduló h félegyeneseket úgy, hogy f az XY oldallal $\alpha$ , g az YZ oldallal $\gamma$ , h pedig a ZX oldallal $\varepsilon$ szöget zárjon be, ekkor f az XZ oldallal $\beta$ , g az YX oldallal $\delta$ , h pedig a ZY oldallal $\zeta$ szöget zár be. Ekkor a segédtétel másik irányát használva azt kapjuk, hogy az f,g,h félegyenesek egy közös U pontban metszik egymást. Az U pontra az iménti eltolások inverzét alkalmazva éppen a megfelelő Q', R', illetve P' ponthoz jutunk.

Statistics:

18 students sent a solution.

5 points: Bálint Dániel, Bodor Bertalan, Éles András, Fonyó Dávid, Huszár Kristóf, Kalina Kende, Lovas Lia Izabella, Nagy 648 Donát.

3 points: 2 students.

2 points: 1 student.

1 point: 4 students.

0 point: 3 students.

Problems in Mathematics of KöMaL, September 2008

18 students sent a solution.
5 points:	Bálint Dániel, Bodor Bertalan, Éles András, Fonyó Dávid, Huszár Kristóf, Kalina Kende, Lovas Lia Izabella, Nagy 648 Donát.
3 points:	2 students.
2 points:	1 student.
1 point:	4 students.
0 point:	3 students.

Already signed up?
New to KöMaL?