Mathematical and Physical Journal
for High Schools
Issued by the MATFUND Foundation
Already signed up?
New to KöMaL?

Problem B. 4112. (October 2008)

B. 4112. A billiards ball at corner A of a rectangular billiards table ABCD is struck. It starts moving along the angle bisector. It rebounds from the sides CD, BC and finally AB, and collides head-on with a ball that is at the centre of the rectangle. In what other direction is it possible to strike the ball at point A, so that it rebounds from three different sides and then hits the ball at the centre head-on?

(4 pont)

Deadline expired on November 17, 2008.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás: Vizsgáljuk meg általában, hogy egy téglalap alakú XYZV biliárdasztal X csúcsából hogyan lökhetünk el egy golyót úgy, hogy három különböző oldalról visszapattanva telibe találja az O középpontban álló golyót. Szimmetria okok miatt feltesszük, hogy a golyó először a ZV oldal P pontjáról pattan vissza. Tegyük fel, hogy ezután az XY oldal Q pontjáról pattan tovább. Innen nyilván az YZ oldal egy R pontjába kell kerülnie. Legyen S és T a VZ oldal azon két pontja, amelyre RS, illetve YT párhuzamos PQ-val. Az XYTP szimmetrikus trapéz a belsejében tartalmazza az O pontot, míg az RS szakasz a trapézon kívül helyezkedik el, vagyis nem haladhat át az O ponton. Mivel az R pont érintése után a golyónak az RS szakaszon kell továbbhaladnia, ez a lehetőség nem jöhet szóba.

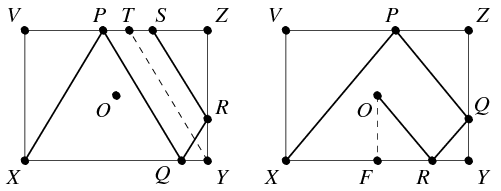
A golyó tehát a P pont után először az YZ oldal egy Q pontjáról pattan tovább, majd az XY oldal egy R pontjának érintése után érkezik meg az O pontba. Legyen az XV oldal hossza a, az XY oldalé b, az XY oldal felezőpontja pedig F. Tegyük fel, hogy a P pont a VZ oldalt x:(1-x) arányban osztja, vagyis VP=xb, PZ=(1-x)b. Az XVP, QZP, QYR és OFR derékszögű háromszögek hasonlóságát felhasználva rendre azt kapjuk, hogy

ZQ=\frac{1-x}{x}a,\quad YQ=a-ZQ=\frac{2x-1}{x}a,\quad YR=(2x-1)b,\quad

FR=\frac{b}{2}-YR=\frac{3-4x}{2}b,\quad \frac{a}{2}=OF=\frac{3-4x}{2x}a.

Az utolsó összefüggés alapján x=3/5.

Rátérve a konkrét feladatra, ha az A csúcsból a szögfelező irányában ellökött golyó a CD oldalt a P pontban találja el, akkor AD=DP=(3/5)CD. Ezenkívül még az jön szóba, hogy a golyó a BC, CD majd AD oldalakról visszapattanva találja el a középen álló golyót, ehhez pedig a BC oldal azon Q pontja irányába kell meglökni, amelyre BQ=(3/5)BC=(9/25)AB. Vagyis a golyót az AB oldallal {\hbox {\rm arctg}}(9/25)\approx 19,8^\circ-os szöget bezáró irányban kell ellökni.

Statistics:

153 students sent a solution.
4 points:Ágoston Tamás, Aujeszky Tamás, Beke Lilla, Bencskó György Árpád, Blázsik Zoltán, Bodor Bertalan, Bóra Eszter, Bősze Zsuzsanna, Cséke Balázs, Csizmadia Luca, Csuka Róbert, Éles András, Énekes Péter, Fonyó Dávid, Frankl Nóra, Fülep Csilla, Gévay Gábor, Hajdók Soma, Horowitz Gábor, Janzer Olivér, Keresztfalvi Tibor, Kiss 232 Dóra, Kiss 427 Borbála, Kiss 542 Robin, Kiss 902 Melinda Flóra, Kiss Boldizsár, Klenk 191 Blanka, Lelkes Ádám, Lenger Dániel, Lovas Lia Izabella, Mezei Márk, Nagy 123 Balázs, Nagy 127 Márton, Nagy 648 Donát, Ódor Gergely, Palincza Richárd, Rácz Zoltán, Somogyi Ákos, Vadon Viktória, Varga 171 László, Varga 777 Ádám, Weisz Ágoston, Weisz Gellért, Zelena Réka.
3 points:62 students.
2 points:27 students.
1 point:11 students.
0 point:9 students.

Problems in Mathematics of KöMaL, October 2008