 Problem B. 4117. (October 2008)
Problem B. 4117. (October 2008)
B. 4117. Three lines passing through a point P are cut by two other lines at the points A, B, C and A', B', C', respectively. Prove that , where the ratios are considered directed.
(5 pont)
Deadline expired on November 17, 2008.
Sorry, the solution is available only in Hungarian. Google translation
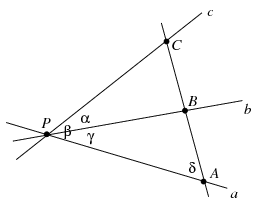
Megoldás: Jelölje a három egyenest értelemszerűen a,b,c. A jelölést ciklikusan megváltoztatva a baloldali kifejezés nem változik, a körüljárási irányt megfordítva pedig ellentettjére változik. Ezért nyugodtan feltehetjük, hogy az A,B,C pontok az ábrán látható módon helyezkednek el. Azt is feltehetjük, hogy a PA,PB,PC szakaszok hosszának előjele pozitív. Az APB,APC,BPC szögeket jelölje rendre  ,
, ,
, , az CAP szöget pedig
, az CAP szöget pedig  .
.
Előjelesen számolva AA'+A'P=AP, BB'+B'P=BP és CC'+C'P=CP. Ezért mindkét oldalhoz a vektort hozzáadva a bizonyítandó állítást
alakra hozhatjuk. A PAB és PAC háromszögekre a szinusz tételt felírva a sin  /sin
/sin  =AB/PB, sin
=AB/PB, sin  /sin
/sin  =AC/PC összefüggéseket kapjuk, ahonnan
=AC/PC összefüggéseket kapjuk, ahonnan
Ugyanezt a PBC és PAC háromszögekre elvégezve pedig
adódik. Figyelembe véve, hogy az ,
,
vektorok egy egyenesre esnek, de az utóbbi iránya ellentétes az első kettőével, láthatjuk, hogy igazából a
állítást kellene igazolni.
Tegyük fel először, hogy az A',B',C' pontok az A,B,C pontokhoz hasonlóan helyezkednek el, vagyis PA', PB' és PC' is pozitív. A nevezőkkel felszorozva, a kapott
PB'.PC'.sin  -PA'.PC'.sin
-PA'.PC'.sin  +PA'.PB'.sin
+PA'.PB'.sin  =0
=0
állítás nyilván igaz, hiszen azt fejezi ki, hogy a PAC háromszög területe megegyezik a PAB és PBC háromszögek területének összegével. Ugyanez a helyzet akkor is, ha PA', PB' és PC' is negatív.
Tegyük fel most, hogy a második egyenes a három egyenest b,c,a sorrendben metszi úgy, hogy PA' negatív, PB' és PC' pedig pozitív. Ekkor a B'PC' szög továbbra is  , a B'PA', illetve C'PA' szög pedig 180o-
, a B'PA', illetve C'PA' szög pedig 180o- , illetve 180o-
, illetve 180o- lesz. A már igazolt állítást alkalmazhatjuk oly módon, hogy az A' pont szerepét B', a B' pontét C', a C' pontét pedig A' veszi át.
lesz. A már igazolt állítást alkalmazhatjuk oly módon, hogy az A' pont szerepét B', a B' pontét C', a C' pontét pedig A' veszi át.
Így azt kapjuk, hogy
ez pedig ekvivalens a bizonyítandó állítással, hiszen sin x=sin (180o-x) és |PA'|=-PA'. A fennmaradó esetek is hasonló gondolattal könnyen elintézhetők.
Statistics:
27 students sent a solution. 5 points: Baranyai Zoltán, Blázsik Zoltán, Bodor Bertalan, Böőr Katalin, Csere Kálmán, Énekes Péter, Fekete Dorottya, Fonyó Dávid, Frankl Nóra, Huszár Kristóf, Lovas Lia Izabella, Márki Róbert, Márkus Bence, Perjési Gábor, Ratku Antal, Somogyi Ákos, Szabó 928 Attila, Varga 171 László, Weisz Ágoston. 4 points: Bóra Eszter, Cséke Balázs, Éles András, Horváth Dániel, Keresztfalvi Tibor, Nagy 648 Donát. 3 points: 1 student. 0 point: 1 student.
Problems in Mathematics of KöMaL, October 2008
