 Problem B. 4128. (November 2008)
Problem B. 4128. (November 2008)
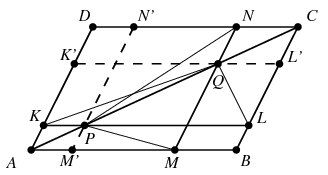
B. 4128. P and Q are two different points on the diagonal AC of a parallelogram ABCD. The line through P parallel to AB intersects the sides BC and AD at K and L, and the line through Q parallel to BC intersects the sides AB and CD at M and N. Show that the areas of the triangles PNM and QKL are equal.
(3 pont)
Deadline expired on December 15, 2008.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Húzzuk meg a P, illetve Q ponton át a paralelogramma másik oldalával párhuzamos egyenest is az ábra szerint. Ha a PQ szakasz hossza az AC átló hosszának 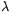 -szorosa, akkor a párhuzamos szelők tételének értelmében az MM' szakasz hossza is
-szorosa, akkor a párhuzamos szelők tételének értelmében az MM' szakasz hossza is 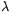 -szorosa az AB oldal hosszának. Ezért az MNN'M' paralelogramma területe
-szorosa az AB oldal hosszának. Ezért az MNN'M' paralelogramma területe 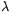 -szorosa az ABCD paralelogramma területének, míg a PNM háromszög területe ennek fele lesz. Ugyanezt az indoklást a KLL'K' paralelogrammával elmondva kapjuk, hogy a QKL háromszög területe is (
-szorosa az ABCD paralelogramma területének, míg a PNM háromszög területe ennek fele lesz. Ugyanezt az indoklást a KLL'K' paralelogrammával elmondva kapjuk, hogy a QKL háromszög területe is (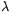 /2)-szöröse az ABCD paralelogramma területének.
/2)-szöröse az ABCD paralelogramma területének.
Statistics:
122 students sent a solution. 3 points: 97 students. 2 points: 2 students. 1 point: 10 students. 0 point: 11 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, November 2008
