 Problem B. 4136. (December 2008)
Problem B. 4136. (December 2008)
B. 4136. Given a convex quadrilateral, construct a rhombus with vertices lying on the sides of the quadrilateral, and sides parallel to the diagonals of the quadrilateral.
(3 pont)
Deadline expired on January 15, 2009.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Legyen P,Q,R és S az ABCD konvex négyszög AB, BC, CD, illetve DA oldalának egy-egy pontja. Ha PQ és RS párhuzamos az AC átlóval, QR pedig a BD átlóval, akkor
AP:PB=CQ:QB=CR:RD=AS:SD,
vagyis PS is párhuzamos a BD átlóval, tehát a PQRS négyszög paralelogramma. A P pontot megválasztásánál tehát arra kell ügyelnünk, hogy amennyiben a Q,R,S pontok a fenti párhuzamossági követelményeknek eleget tesznek, PQ=QR teljesüljön. Lévén ilyen esetben
a PQ=QR feltétel pontosan akkor teljesül, ha AP:PB=AC:BD.
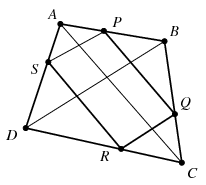
Ezek alapján a szerkesztés menete a következő lehet. Az AC átló C-n túli meghosszabbítására felmérjük a BD szakaszt, így kapjuk a D' pontot. A BD' egyenessel C-n át húzott párhuzamos metszi ki az AB oldalból azt a P pontot, amelyre AP:PB=AC:BD. Ezek után Q,R és S már egyszerűen megkapható, a feladatnak minden esetben pontosan egy megoldása létezik.
Statistics:
105 students sent a solution. 3 points: Ágoston Péter, Béres Ferenc, Botos Csongor, Czeller Ildikó, Deák Zsolt, Dinh Hoangthanh Attila, Éles András, Fülep Csilla, Gyarmati Máté, Hegedűs Csaba, Horowitz Gábor, Huszár Kristóf, Iglói Gábor, Janosov Milán, Janzer Olivér, Keresztfalvi Tibor, Kiss 232 Dóra, Kiss Boldizsár, Kószó Simon, Kovács 888 Adrienn, Kovács 999 Noémi, Lantos Tamás, Mezei Márk, Morapitiye Sunil, Nguyen Milán, Réti Dávid, Scharle András, Weisz Ágoston, Weisz Gellért, Zsakó András. 2 points: 58 students. 1 point: 3 students. 0 point: 11 students. Unfair, not evaluated: 3 solutionss.
Problems in Mathematics of KöMaL, December 2008
