 Problem B. 4139. (December 2008)
Problem B. 4139. (December 2008)
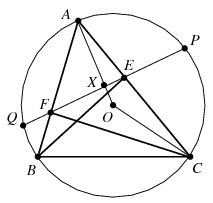
B. 4139. Two altitudes of an acute-angled triangle ABC are BE and CF. Line EF intersects the circumscribed circle at P and Q. Prove that AP=AQ.
(4 pont)
Deadline expired on January 15, 2009.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: A körülírt kör középpontja legyen O, az A-ból az EF egyenesre bocsájtott merőleges talppontja X, az ABC szöget pedig szokás szerint jelölje  . Ekkor
. Ekkor , vagyis
. Mivel E és F egyaránt a BC szakaszra emelt Thalesz-körön helyezkednek el, a BCEF négyszög húrnégyszög és így
. Ebből adódik, hogy
, vagyis az AX egyenes áthalad az O ponton. Más szóval az AX egyenes a kör egy szimmetriatengelye, ami felezi a rá merőleges PQ húrt, amiért is az AXP és AXQ derékszögű háromszögek egybevágóak, AP=AQ.
Statistics:
79 students sent a solution. 4 points: 68 students. 3 points: 2 students. 2 points: 3 students. 1 point: 3 students. 0 point: 1 student. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, December 2008
