 Problem B. 4147. (January 2009)
Problem B. 4147. (January 2009)
B. 4147. Prove that any right angled triangle can be extended to a rectangle by attaching to its sides three right angled triangles which are similar to each other.
(3 pont)
Deadline expired on February 16, 2009.
Sorry, the solution is available only in Hungarian. Google translation
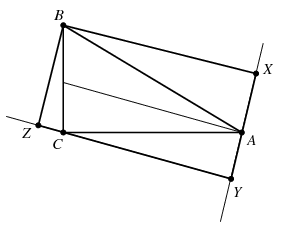
Megoldás: Válasszuk ki az ABC derékszögű háromszög egyik hegyesszögű csúcsát (A), és az erre illeszkedő külső szögfelezőre állítsunk merőlegest a másik két csúcsból az ábra szerint. Ezek talppontját jelölje X és Y. Így az egymáshoz hasonló ABX és ACY derékszögű háromszögekhez jutunk. A B csúcsból az YC egyenesre állított merőleges talppontja legyen Z. Mivel az XBC szög nagysága  /2+
/2+ <90o, a C derékszögű csúcs a ZY szakasz belső pontja lesz. Minthogy pedig az ACY és BCZ szögek derékszögre egészítik ki egymást, a CBZ derékszögű háromszög is hasonló ACY-hoz, az ABC háromszöget ezzel a három egymáshoz hasonló derékszögű háromszöggel kiegészítve az XYZB téglalapot nyerjük.
<90o, a C derékszögű csúcs a ZY szakasz belső pontja lesz. Minthogy pedig az ACY és BCZ szögek derékszögre egészítik ki egymást, a CBZ derékszögű háromszög is hasonló ACY-hoz, az ABC háromszöget ezzel a három egymáshoz hasonló derékszögű háromszöggel kiegészítve az XYZB téglalapot nyerjük.
Statistics:
109 students sent a solution. 3 points: 78 students. 2 points: 23 students. 1 point: 3 students. 0 point: 3 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, January 2009
