 Problem B. 4152. (February 2009)
Problem B. 4152. (February 2009)
B. 4152. Given n different subsets of the set of numbers 1,2,3,...,n, prove that there exists a number, such that if it is left out of each subset, the remaining subsets will still be different.
(4 pont)
Deadline expired on March 16, 2009.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Tegyük fel, hogy nem igaz az állítás, vagyis minden 1 i
i n esetén található az adott halmazok között egy Ai és egy Bi halmaz úgy, hogy
n esetén található az adott halmazok között egy Ai és egy Bi halmaz úgy, hogy , de Bi=Ai
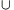 {i}. Tekintsük az adott halmazokat egy gráf csúcsainak, melyben minden i-re az Ai és Bi halmazokat összekötöttünk egy ei éllel. Ennek az n szögpontú, nyilván egyszerű gráfnak pontosan n éle van, tehát található benne egy kör, vagyis az adott halmazoknak egy olyan
{i}. Tekintsük az adott halmazokat egy gráf csúcsainak, melyben minden i-re az Ai és Bi halmazokat összekötöttünk egy ei éllel. Ennek az n szögpontú, nyilván egyszerű gráfnak pontosan n éle van, tehát található benne egy kör, vagyis az adott halmazoknak egy olyan sorozata, ahol az indexekkel modulo k számolva, minden i-re Hi és Hi+1 között halad egy él. A kör irányítását megfelelően választva feltehetjük, hogy H1=Aj, H2=Bj valamely 1
 j
j n esetén. Ekkor a j szám nem eleme a H1 halmaznak, de eleme H2-nek. Mivel i
n esetén. Ekkor a j szám nem eleme a H1 halmaznak, de eleme H2-nek. Mivel i 1 esetén Hi és Hi+1 között már nem az ej él vezet, ebből j
1 esetén Hi és Hi+1 között már nem az ej él vezet, ebből j H3, majd ugyanígy
H3, majd ugyanígy , végül j
 H1 adódik. Ez az ellentmodás bizonyítja, hogy az állítás mégiscsak igaz kellett legyen.
H1 adódik. Ez az ellentmodás bizonyítja, hogy az állítás mégiscsak igaz kellett legyen.
Statistics:
54 students sent a solution. 4 points: Ágoston Tamás, Aujeszky Tamás, Backhausz Tibor, Beke Lilla, Blázsik Zoltán, Bodor Bertalan, Damásdi Gábor, Éles András, Fonyó Dávid, Frankl Nóra, Huszár Kristóf, Kiss 902 Melinda Flóra, Kiss 991 Mátyás, Lovas Lia Izabella, Mészáros András, Nagy 111 Miklós, Nagy 648 Donát, Perjési Gábor, Strenner Péter, Varga 171 László, Vuchetich Bálint, Weisz Ágoston, Weisz Gellért. 3 points: Énekes Péter, Szabó 124 Zsolt, Tubak Dániel. 2 points: 5 students. 1 point: 3 students. 0 point: 17 students. Unfair, not evaluated: 3 solutionss.
Problems in Mathematics of KöMaL, February 2009
