 Problem B. 4181. (April 2009)
Problem B. 4181. (April 2009)
B. 4181. The opposite edges of a tetrahedron are equal in length and they pairwise enclose equal angles. Prove that the tetrahedron is regular.
(4 pont)
Deadline expired on May 15, 2009.
Sorry, the solution is available only in Hungarian. Google translation
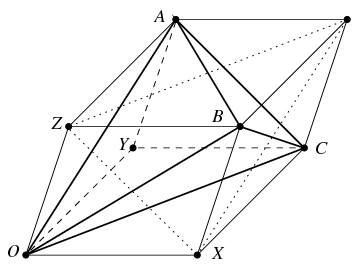
Megoldás: Legyen a tetraéder egyik csúcsa O, a másik három pedig A,B,C. Tekintsük azon X,Y,Z pontokat, amelyekre
ekkor ,
és
. Ezek szerint az A,B,C pontok O-val másodszomszédos csúcsai annak a parallelepipedonnak, amelynek egyik csúcsa O, annak szomszédai pedig X,Y és Z. A tetraéder élei ennek a parallelepipedonnak lapátlói lesznek. A szemközti élek egyenlősége azt jelenti, hogy a parallelepipeon lapjai olyan parallelogrammák, melyek mindegyikében a két átló egyforma hosszú. Más szóval, a parallelepipeon lapjai téglalapok, a szögek egyenlőségéből pedig arra következtethetünk, hogy ezek a lapok egybevágóak. Innen már könnyű látni, hogy a parallelepipeon csakis kocka lehet, a tetraéder pedig valóban szabályos.
Statistics:
31 students sent a solution. 4 points: Blázsik Zoltán, Bodor Bertalan, Csizmadia Luca, Dunay Luca, Frankl Nóra, Győrfi 946 Mónika, Janosov Milán, Jernei Tamás, Kovács 235 Gábor, Márkus Bence, Mészáros András, Milánkovich Dorottya, Németh Bence, Perjési Gábor, Tóth 222 Barnabás, Varga 171 László, Vuchetich Bálint. 3 points: Bősze Zsuzsanna, Cséke Balázs, Gyarmati Máté, Kiss Boldizsár, Lajos Mátyás, Nagy 111 Miklós, Nguyen Milán, Strenner Péter, Szenczi Zoltán. 2 points: 1 student. 0 point: 1 student. Unfair, not evaluated: 3 solutionss.
Problems in Mathematics of KöMaL, April 2009
