Problem B. 4186. (May 2009)

B. 4186. In an acute-angled triangle ABC, circles are drawn around the altitudes as diameters. In each circle, a chord is drawn that is perpendicular to the appropriate altitude and passes through the orthocentre of the triangle. Prove that the three chords obtained in this way are equal in length.

(3 pont)

Deadline expired on June 15, 2009.

Sorry, the solution is available only in Hungarian. Google translation

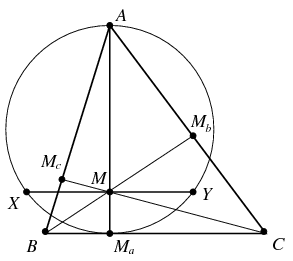
Megoldás. A szokásos jelöléseket használva az \(\displaystyle AM_a\) magasságvonalra merőleges \(\displaystyle XY\) húr hossza, lévén \(\displaystyle AXM_a\) és \(\displaystyle AYM_a\) egybevágó derékszögű háromszögek, a magasságtétel alapján

\(\displaystyle XY=2\sqrt{AM\cdot MM_a}.\)

Mivel az \(\displaystyle b=2R\sin\beta\), \(\displaystyle c=2R\sin\gamma\) összefüggések miatt

\(\displaystyle AM=\frac{AM_c}{\sin\beta}=\frac{b\cos\alpha}{\sin\beta}=2R\cos\alpha\)

és

\(\displaystyle MM_a=\frac{BM_a}{\tg\gamma}=\frac{c\cos\beta}{\tg\gamma}=2R\cos\beta\cos\gamma,\)

kapjuk, hogy \(\displaystyle XY=4R\sqrt{\cos\alpha\cos\beta\cos\gamma}\).

Szimmetria okok miatt a másik két húr hossza is ugyanennyi kell legyen.

Statistics:

48 students sent a solution.
3 points:	Ágoston Péter, Beke Lilla, Béres Ferenc, Botos Csongor, Böőr Katalin, Bősze Zsuzsanna, Csere Kálmán, Damásdi Gábor, Deák Zsolt, Dinh Hoangthanh Attila, Dunay Luca, Gyarmati Máté, Huszár Kristóf, Janosov Milán, Janzer Olivér, Keresztfalvi Tibor, Kiss 902 Melinda Flóra, Korondi Zénó, Kovács 235 Gábor, Kovács 888 Adrienn, Kovács 999 Noémi, Lantos Tamás, Lenger Dániel, Loose Lilla, Maknics András, Márki Róbert, Mészáros András, Mezei Márk, Muszka Balázs, Nagy 123 Balázs, Nagy Róbert, Németh 217 Balázs, Rácz Zoltán, Strenner Péter, Szabó 928 Attila, Szenczi Zoltán, Tóth Tekla, Vajk Dóra, Varju 105 Tamás, Weisz Ágoston, Weisz Gellért, Welsz Edit, Zelena Réka, Zsakó András.
2 points:	Kiss Boldizsár.
1 point:	1 student.
Unfair, not evaluated:	2 solutionss.

Problems in Mathematics of KöMaL, May 2009