 Problem B. 4188. (May 2009)
Problem B. 4188. (May 2009)
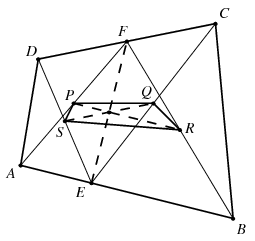
B. 4188. Sides AB and CD of a quadrilateral ABCD are not parallel. Let E and F, respectively, be interior points of these sides. Prove that the midpoints of the line segments AF, CE, BF and DE form a convex quadrilateral whose area is independent of the choice of points E and F.
Kvant
(4 pont)
Deadline expired on June 15, 2009.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az ábra jelöléseit használva, a \(\displaystyle PR\) szakasz, mint az \(\displaystyle ABF\) háromszög egyik középvonala, párhuzamos az \(\displaystyle AB\) oldallal, fele olyan hosszú, és áthalad az \(\displaystyle EF\) szakasz felezőpontján. Hasonlóképpen a \(\displaystyle QS\) szakasz párhuzamos a \(\displaystyle CD\) oldallal, fele olyan hosszú, és szintén áthalad az \(\displaystyle EF\) szakasz felezőpontján. Az \(\displaystyle EF\) szakasz felezőpontja ezek szerint belső pontja mind a \(\displaystyle PR\), mind a \(\displaystyle QS\) szakasznak, melyek egymással nem párhuzamosak, hanem ugyanakkora \(\displaystyle \vartheta\) szöget zárnak be, mint az \(\displaystyle AB\) és \(\displaystyle CD\) egyenesek. Ezért a \(\displaystyle P,Q,R,S\) pontok, ebben a sorrendben, valóban egy konvex négyszög csúcsai. Ennek területe pedig
\(\displaystyle t=\frac{1}{2}\cdot PR\cdot QS\cdot \sin\vartheta=\frac{AB\cdot CD\cdot \sin\vartheta}{8},\)
ami tényleg független az \(\displaystyle E,F\) pontok helyzetének megválasztásától.
Statistics:
57 students sent a solution. 4 points: Beke Lilla, Blázsik Zoltán, Bodor Bertalan, Dinh Hoangthanh Attila, Dudás 002 Zsolt, Éles András, Énekes Péter, Frankl Nóra, Gyarmati Máté, Huszár Kristóf, Kiss 902 Melinda Flóra, Kovács 888 Adrienn, Kovács 999 Noémi, Lenger Dániel, Lovas Lia Izabella, Mailach Petra, Márkus Bence, Mezei Márk, Nagy 648 Donát, Neukirchner Elisabeth, Perjési Gábor, Somogyi Ákos, Tuan Nhat Le, Varga 171 László, Varju 105 Tamás. 3 points: 27 students. 2 points: 3 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, May 2009
