Problem B. 4190. (May 2009)

B. 4190. The solid shown in the Figure is made up of six congruent cubes glued together. Is it possible to fill the space without gaps and overlaps with congruent copies of this solid?

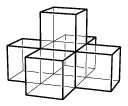
(5 pont)

Deadline expired on June 15, 2009.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyenek a kockák élei egységnyi hosszúságúak. Rögzítsünk a térben egy derékszögű koordinátarendszert, és tekintsük ebben az

\(\displaystyle A_0(0;0;0), A_1(1;0;0), A_2(0;1;0), A_3(0;0;1), A_4(0;-1;0), A_5(-1;0;0)\)

pontokat. Tetszőleges \(\displaystyle v(x;y;z)\) vektor esetén tekintsük az

\(\displaystyle {\mathcal X}_v=\{A_0+v,A_1+v,A_2+v,A_3+v,A_4+v,A_5+v\}\)

halmazt, ezek nyilván páronként egybevágó halmazok. Ha \(\displaystyle x,y,z\) olyan egész számok, amelyekre \(\displaystyle x+2y+3z\) osztható 6-tal, akkor tetszőleges \(\displaystyle i\)-re teljesül, hogy az \(\displaystyle A_i+v\) pont \(\displaystyle x',y',z'\) kordinátáira az \(\displaystyle x'+2y'+3z'\) szám 6-tal osztva éppen \(\displaystyle i\) maradékot ad. Az is könnyen ellenőrizhető, hogy tetszőleges \(\displaystyle x',y',z'\) egész számok esetén, ha \(\displaystyle x'+2y'+3z'\) 6-tal osztva \(\displaystyle i\) maradékot ad, akkor van pontosan egy olyan \(\displaystyle v(x;y;z)\) vektor, melynek koordinátái egészek, \(\displaystyle x+2y+3z\) 6-tal osztható, és az \(\displaystyle A_i+v\) pont koordinátái éppen \(\displaystyle x',y',z'\). Ez éppen azt jelenti, hogy azon \(\displaystyle {\mathcal X_v}\) halmazok, ahol \(\displaystyle x,y,z\) olyan egész számok, amelyekre \(\displaystyle x+2y+3z\) osztható 6-tal, együttesen tartalmazzák az összes rácspontot, mégpedig minden rácspont ezen halmazok közül pontosan egyhez tartozik hozzá. Mármost ha minden egyes megfelelő \(\displaystyle v\) vektorra a szóban forgó test egy példányát úgy helyezzük el a térben, hogy az őt felépítő kis kockák középpontjai az \(\displaystyle {\mathcal X_v}\) halmaz elemeivel essenek egybe (ami nyilván megtehető), akkor ezek a példányok hézagmentesen és átfedések nélkül fogják a teret kitölteni.

Statistics:

45 students sent a solution.
5 points:	Ágoston Tamás, Beke Lilla, Blázsik Zoltán, Bodor Bertalan, Csizmadia Luca, Damásdi Gábor, Deák Zsolt, Dinh Hoangthanh Attila, Dudás 002 Zsolt, Éles András, Fonyó Dávid, Huszár Kristóf, Kiss 902 Melinda Flóra, Kiss Boldizsár, Kovács 888 Adrienn, Kovács 999 Noémi, Lenger Dániel, Lovas Lia Izabella, Márkus Bence, Mester Márton, Mészáros András, Mezei Márk, Nagy 111 Miklós, Nagy Róbert, Palincza Richárd, Perjési Gábor, Somogyi Ákos, Varga 171 László, Vuchetich Bálint, Weisz Ágoston.
4 points:	Baranyai Zoltán, Csere Kálmán, Frankl Nóra, Keresztfalvi Tibor, Nagy 648 Donát, Neukirchner Elisabeth, Nguyen Milán, Paripás Viktor.
3 points:	4 students.
2 points:	3 students.

Problems in Mathematics of KöMaL, May 2009