Problem B. 4194. (September 2009)

B. 4194. The angle at vertex C of a triangle is a right angle. The angle bisector and altitude drawn from C intersect the circumscribed circle at D and E, respectively. The not shorter leg of the triangle is b. Show that the length of the broken line CDE is .

(4 pont)

Deadline expired on October 12, 2009.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen a körülírt kör átmérője egységnyi, a \(\displaystyle b\) befogó melleti szög pedig \(\displaystyle \alpha\le 45^\circ\). Mivel az átfogó éppen a kör átmérője, \(\displaystyle b=\cos\alpha\).

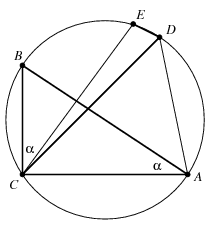
Az ábra jelöléseit használva, a \(\displaystyle BCD\) és a \(\displaystyle BAD\) szög egyaránt \(\displaystyle 45^\circ\)-os, vagyis a \(\displaystyle CD\) húr az \(\displaystyle A\) pontból \(\displaystyle 45^\circ+\alpha\), az \(\displaystyle ED\) húr pedig a \(\displaystyle C\) pontból \(\displaystyle 45^\circ-\alpha\) szög alatt látszik. Ezért valóban

\(\displaystyle CD+DE=\sin(45^\circ+\alpha)+\sin(45^\circ-\alpha)=2\sin45^\circ\cos\alpha= \sqrt{2}\cos\alpha=b\sqrt{2}.\)

Statistics:

138 students sent a solution.
4 points:	127 students.
3 points:	7 students.
2 points:	1 student.
1 point:	1 student.
0 point:	2 students.

Problems in Mathematics of KöMaL, September 2009