 Problem B. 4205. (October 2009)
Problem B. 4205. (October 2009)
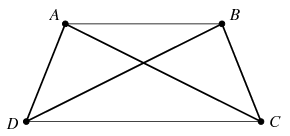
B. 4205. A, B, C, D are moving points in the plane, such that AD=BC=2 and AC=BD=4 remain valid, and the line segments AC and BD intersect each other for all positions of the points. How does the distance CD depend on the distance AB?
(3 pont)
Deadline expired on November 10, 2009.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az \(\displaystyle ABCD\) trapézban \(\displaystyle BAD\sphericalangle+CDA\sphericalangle=180^\circ\), vagyis \(\displaystyle \cos BAD\sphericalangle+\cos CDA\sphericalangle=0\). A koszinusz tétel szerint
\(\displaystyle \frac{AB^2+2^2-4^2}{2\cdot 2AB}+\frac{CD^2+2^2-4^2}{2\cdot 2CD}=0,\)
ahonnan felszorzás és rendezés után az
\(\displaystyle (AB+CD)(AB\cdot CD-12)=0\)
egyenlőségre jutunk, vagyis \(\displaystyle CD=12/AB\).
Statistics:
115 students sent a solution. 3 points: 76 students. 2 points: 8 students. 1 point: 17 students. 0 point: 11 students. Unfair, not evaluated: 3 solutionss.
Problems in Mathematics of KöMaL, October 2009
