 Problem B. 4207. (October 2009)
Problem B. 4207. (October 2009)
B. 4207. Is it true that every polygon has a vertex from which it is possible to draw a diagonal in the inside of the polygon to a non-adjacent vertex that is closest to it? (Suggested by P. Maga)
(4 pont)
Deadline expired on November 10, 2009.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az állítás nem igaz, amint azt az alábbi ellenpélda mutatja. Vegyük fel az \(\displaystyle A,B,C,D\), \(\displaystyle E,F\) pontokat az ábrán látható módon úgy, hogy \(\displaystyle AF=AE=BE=BD=CD=1\) és \(\displaystyle AB=BC=DE=EF=\sqrt{2}\), ekkor \(\displaystyle AEF\), \(\displaystyle AEB\), \(\displaystyle BED\) és \(\displaystyle BDC\) egyenlőszárú derékszögű háromszögek.
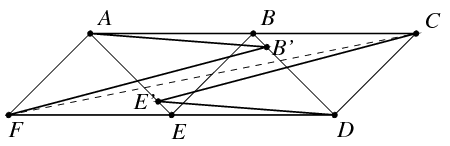
A \(\displaystyle CF\) szakasz \(\displaystyle BD\)-vel vett metszéspontját \(\displaystyle B\)-vel összekötő szakasz felezőpontja legyen \(\displaystyle B'\), \(\displaystyle E'\) pedig legyen ennek a pontnak a \(\displaystyle CF\) szakasz felezőpontjára vonatkozó tükörképe. Könnyen ellenőrizhetjük, hogy \(\displaystyle CF>DF=CA>B'F=CE'>DA>B'A=DE'>CB'>B'E'>CD>B'D\). Ezért az \(\displaystyle AB'FDE'C\) középpontosan szimmetrikus hatszögben a \(\displaystyle B'\) csúcshoz legközelebb eső csúcs \(\displaystyle D\), a \(\displaystyle C\) csúcshoz legközelebb eső csúcs \(\displaystyle D\), a \(\displaystyle D\) csúcshoz legközelebb eső csúcs pedig \(\displaystyle B'\), azonban sem a \(\displaystyle B'D\), sem a \(\displaystyle CD\) átló nem marad a sokszög belsejében. Az \(\displaystyle A,E',F\) csúcsok esetében pedig elegendő szimmetria okokra hivatkozni.
Statistics:
68 students sent a solution. 4 points: Ábrahám Zsófia, Bálint Csaba, Bauer Barbara, Bősze Zsuzsanna, Csapó Botond Dániel, Cséke Balázs, Damásdi Gábor, Dudás 002 Zsolt, Éles András, Énekes Péter, Gyarmati Máté, Hajnal Péter János, Karkus Zsuzsa, Keresztfalvi Tibor, Kunos Vid, Márkus Bence, Mester Márton, Mészáros András, Nagy Róbert, Nagy-György Péter, Németh Bence, Perjési Gábor, Somogyi Ákos, Szenczi Zoltán, Varju 105 Tamás, Vogronics Patrik, Weisz Ágoston, Zelena Réka. 3 points: Jaksa Péter, Magyari Ábel. 1 point: 7 students. 0 point: 24 students. Unfair, not evaluated: 7 solutionss.
Problems in Mathematics of KöMaL, October 2009
