 Problem B. 4213. (November 2009)
Problem B. 4213. (November 2009)
B. 4213. What is the largest possible number of sides of a convex polygon which can be dissected into right-angled triangles with acute angles of 30 and 60 degrees?
(4 pont)
Deadline expired on December 10, 2009.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Tegyük fel, hogy egy konvex sokszög feldarabolható a kí vánt módon. Mivel a felosztásban szereplő háromszögek minden szöge \(\displaystyle 30^\circ\) egész számú többszöröse, ugyanez igaz a sokszög minden egyes szögére, vagyis azok legfeljebb \(\displaystyle 150^\circ\)-os szögek lehetnek. Ennek megfelelően a sokszög minden külső szöge legfeljebb \(\displaystyle 30^\circ\)-os. Mivel ezek összege \(\displaystyle 360^\circ\), a sokszögnek legfeljebb 12 oldala lehet.
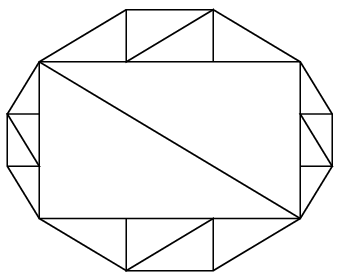
Az ábrán egy megfelelő 12 oldalú sokszöget láthatunk.
Ez úgy keletkezett, hogy először két megfelelő egybevágó háromszöget egy téglalappá illesztettünk össze. Ezután a hosszabbik oldalak fölé harmadekkora háromszögekből összerakott szimmetrikus trapézokat illesztettünk, és hasonlóképpen jártunk el a rövidebb oldalakat illetően is.
Statistics:
89 students sent a solution. 4 points: Ábrahám Zsófia, Ágoston Péter, Ágoston Tamás, Bauer Barbara, Beke Lilla, Csere Kálmán, Csuka Róbert, Czipó Bence, Damásdi Gábor, Dudás 002 Zsolt, Éles András, Énekes Péter, Fehér Péter, Hajnal Péter János, Janzer Olivér, Karkus Zsuzsa, Keresztfalvi Tibor, Kiss 232 Dóra, Kiss 902 Melinda Flóra, Kovács Attila, Kunos Vid, Lajos Mátyás, László 002 Dávid, Márkus Bence, Medek Ákos, Mester Márton, Mészáros András, Nagy 111 Miklós, Nagy Róbert, Nagy-György Péter, Orsós Ferenc Richárd, Perjési Gábor, Sándor Áron Endre, Sieben Bertilla, Somogyi Ákos, Szabó 124 Zsolt, Szabó 928 Attila, Szenczi Zoltán, Szili László, Szórádi Márk, Varga 311 Róbert, Varnyú József, Weimann Richárd, Weisz Ágoston, Weisz Gellért, Zelena Réka, Zsakó András. 3 points: 24 students. 2 points: 8 students. 1 point: 4 students. 0 point: 6 students.
Problems in Mathematics of KöMaL, November 2009
