 Problem B. 4236. (January 2010)
Problem B. 4236. (January 2010)
B. 4236. Let \(\displaystyle a\), \(\displaystyle b\) and \(\displaystyle c\) be the sides of triangle \(\displaystyle ABC\), let \(\displaystyle f_a\), \(\displaystyle f_b\) and \(\displaystyle f_c\) denote the lengths of the interior angle bisectors, and let \(\displaystyle t_a\), \(\displaystyle t_b\) and \(\displaystyle t_c\) be the segments of the interior angle bisectors that lie inside the circumscribed circle. Show that \(\displaystyle a^2b^2c^2= f_af_bf_ct_at_bt_c\).
(Mathematics Magazine, 1977)
(3 pont)
Deadline expired on February 10, 2010.
Sorry, the solution is available only in Hungarian. Google translation
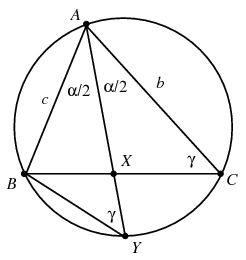
Megoldás. Az ábra jelöléseit használva, a kerületi szögek tétele miatt az \(\displaystyle AYB\) szög ugyanakkora, mint az \(\displaystyle ACB\) szög, vagyis az \(\displaystyle AYB\) háromszög hasonló az \(\displaystyle ACX\) háromszöghöz. Ezért \(\displaystyle AC:AX=AY:AB\), ahonnan \(\displaystyle f_at_a=bc\). Hasonlóképpen kapjuk, hogy \(\displaystyle f_bt_b=ac\) és \(\displaystyle f_ct_c=ab\). E három összefüggést összeszorozva adódik a bizonyítandó állítás.
Statistics:
76 students sent a solution. 3 points: 69 students. 2 points: 3 students. 1 point: 2 students. 0 point: 1 student. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, January 2010
