A B. 4236. feladat (2010. január)

B. 4236. Legyenek az \(\displaystyle ABC\) háromszög oldalai \(\displaystyle a\), \(\displaystyle b\) és \(\displaystyle c\), a belső szögfelezők hossza \(\displaystyle f_a\), \(\displaystyle f_b\) és \(\displaystyle f_c\), a belső szögfelezők körülírt körbe eső szakaszai \(\displaystyle t_a\), \(\displaystyle t_b\) és \(\displaystyle t_c\). Mutassuk meg, hogy \(\displaystyle a^2b^2c^2= f_af_bf_ct_at_bt_c\).

(Mathematics Magazine, 1977)

(3 pont)

A beküldési határidő 2010. február 10-én LEJÁRT.

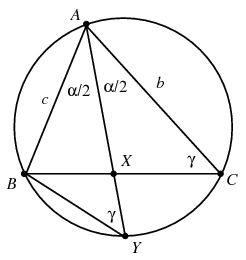
Megoldás. Az ábra jelöléseit használva, a kerületi szögek tétele miatt az \(\displaystyle AYB\) szög ugyanakkora, mint az \(\displaystyle ACB\) szög, vagyis az \(\displaystyle AYB\) háromszög hasonló az \(\displaystyle ACX\) háromszöghöz. Ezért \(\displaystyle AC:AX=AY:AB\), ahonnan \(\displaystyle f_at_a=bc\). Hasonlóképpen kapjuk, hogy \(\displaystyle f_bt_b=ac\) és \(\displaystyle f_ct_c=ab\). E három összefüggést összeszorozva adódik a bizonyítandó állítás.

Statisztika:

76 dolgozat érkezett.
3 pontot kapott:	69 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2010. januári matematika feladatai