A B. 4240. feladat (2010. január)

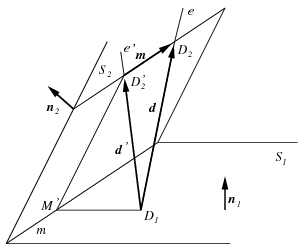
B. 4240. Az S₁ és S₂ síkok metszésvonala m. Az e egyenes az S_i síkot az D_i pontban döfi, az e és S_i szöge pedig $\alpha$ _i. Mutassuk meg, hogy ha D₁ $\ne$ D₂, akkor $\alpha$ ₁> $\alpha$ ₂ pontosan akkor teljesül, ha D₁ közelebb van m-hez mint D₂.

(4 pont)

A beküldési határidő 2010. február 10-én LEJÁRT.

Megoldás. A $\displaystyle D_1\ne D_2$ feltétel azt jelenti, hogy sem $\displaystyle D_1$, sem $\displaystyle D_2$ nem esik az $\displaystyle m$ egyenesre. Ha $\displaystyle D_1$ és $\displaystyle D_2$ ugyanolyan távol helyezkedik el $\displaystyle m$-től, akkor nyilván $\displaystyle \alpha_1=\alpha_2$. Szimmetria okok miatt tehát elég azt megmutatni, hogy ha $\displaystyle D_1$ közelebb van $\displaystyle m$-hez mint $\displaystyle D_2$, akkor $\displaystyle \alpha_1>\alpha_2$. Ez könnyen látható abban az esetben, ha az $\displaystyle e$ egyenes merőleges $\displaystyle m$-re. Ha ugyanis az $\displaystyle m$ egyenes $\displaystyle e$-hez legközelebbi pontja $\displaystyle M$, akkor tekintsük a $\displaystyle D_1MD_2$ háromszöget. Ebben a $\displaystyle D_2$-nél lévő szög kisebb a $\displaystyle D_1$-nél lévő szögnél. Ezért a $\displaystyle D_2$-nél lévő szög mindenképpen hegyesszög, vagyis nem lehet más, mint $\displaystyle \alpha_2$, a $\displaystyle D_1$-nél lévő szög pedig vagy $\displaystyle \alpha_1$, vagy $\displaystyle 180^\circ-\alpha_1$. Az $\displaystyle \alpha_1>\alpha_2$ egyenlőtlenség a második esetben a $\displaystyle D_1MD_2$ háromszögben fennálló $\displaystyle (180^\circ-\alpha_1)+\alpha_2<180^\circ$ egyenlőtlenségből következik.

[] Az általános esetben tekintsük az $\displaystyle S_2$ síkban a $\displaystyle D_2$ pontra illeszkedő, $\displaystyle m$-mel párhuzamos egyenesnek azt a $\displaystyle D_2'$ pontját, amelyre az $\displaystyle e'=D_1D_2'$ egyenes merőleges $\displaystyle m$-re. Legyen az $\displaystyle m$ egyenes $\displaystyle e'$-höz legközelebbi pontja $\displaystyle M'$, a $\displaystyle D_1M'D_2'$ háromszögben a $\displaystyle D_1$-nél, illetve a $\displaystyle D_2'$-nél lévő szög pedig $\displaystyle \alpha_1'$, illetve $\displaystyle \alpha_2'$. Mint ahogyan azt már láttuk, $\displaystyle \alpha_1'> \alpha_2'$. Vezessük be a $\displaystyle {\bf d}=\overrightarrow{D_1D_2}$, $\displaystyle {\bf d}'=\overrightarrow{D_1D_2'}$ és $\displaystyle {\bf m}=\overrightarrow{D_2'D_2}$ vektorokat, ekkor $\displaystyle {\bf d}={\bf d}'+{\bf m}$. Jelölje ezen felül az $\displaystyle S_i$ sík normálvektorát $\displaystyle {\bf n}_i$.

[] Ha az $\displaystyle {\bf n}$ normálvektorral rendelkező $\displaystyle S$ síkkal a vele nem párhuzamos $\displaystyle {\bf v}$ vektor $\displaystyle \alpha$ szöget zár be, akkor (ha a két lehetséges normálvektor közül azt tekintjük, amelyik $\displaystyle {\bf v}$-vel hegyesszöget zár be) a $\displaystyle {\bf v}$ és a $\displaystyle {\bf n}$ vektorok $\displaystyle \beta$ hajlásszögére $\displaystyle \beta=90^\circ-\alpha$, vagyis a skaláris szorzás definíciója szerint $\displaystyle {\bf v}{\bf n}=|{\bf v}|\cdot|{\bf n}|\cos\beta= |{\bf v}|\sin\alpha$. Ennek megfelelően az $\displaystyle {\bf n}_i$ vektorok irányát válasszuk úgy, hogy azok a $\displaystyle {\bf d}$ és $\displaystyle {\bf d}'$ vektorokkal hegyesszöget zárjanak be az ábra szerint. Mivel $\displaystyle 90^\circ\ge\alpha_1'> \alpha_2'$, kapjuk, hogy $\displaystyle \sin\alpha_1'>\sin\alpha_2'$, vagyis $\displaystyle {\bf d}'{\bf n}_1=|{\bf d}'|\sin\alpha_1'>|{\bf d}'|\sin\alpha_2'= {\bf d}'{\bf n}_2$. Mivel az $\displaystyle m$ egyenessel párhuzamos $\displaystyle {\bf m}$ vektor mindekét $\displaystyle {\bf n}_i$ normálvektorra merőleges, $\displaystyle {\bf m}{\bf n}_1= {\bf m}{\bf n}_2={0}$. Ezért $\displaystyle {\bf d}={\bf d}'+{\bf m}$ miatt

$\displaystyle |{\bf d}|\sin\alpha_1={\bf d}{\bf n}_1={\bf d'}{\bf n}_1>{\bf d}'{\bf n}_2 ={\bf d}'{\bf n}_2=|{\bf d}|\sin\alpha_2,$

vagyis $\displaystyle \sin\alpha_1>\sin\alpha_2$, ahonnan $\displaystyle \alpha_1>\alpha_2$ következik.

Statisztika:

26 dolgozat érkezett.

4 pontot kapott: Ágoston Péter, Dudás 002 Zsolt, Éles András, Janzer Olivér, Karkus Zsuzsa, Keresztfalvi Tibor, Kungl Ákos Ferenc, Mészáros András, Mihálka Éva Zsuzsanna, Milánkovich Dorottya, Nagy Balázs, Szabó 928 Attila, Trauttwein Klaudia, Uray Marcell János, Varnyú József.

3 pontot kapott: Böőr Katalin, Nagy Róbert, Weisz Ágoston.

2 pontot kapott: 1 versenyző.

1 pontot kapott: 4 versenyző.

0 pontot kapott: 3 versenyző.

A KöMaL 2010. januári matematika feladatai

26 dolgozat érkezett.
4 pontot kapott:	Ágoston Péter, Dudás 002 Zsolt, Éles András, Janzer Olivér, Karkus Zsuzsa, Keresztfalvi Tibor, Kungl Ákos Ferenc, Mészáros András, Mihálka Éva Zsuzsanna, Milánkovich Dorottya, Nagy Balázs, Szabó 928 Attila, Trauttwein Klaudia, Uray Marcell János, Varnyú József.
3 pontot kapott:	Böőr Katalin, Nagy Róbert, Weisz Ágoston.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	3 versenyző.

Már regisztráltál?
Új vendég vagy?