 Problem B. 4242. (February 2010)
Problem B. 4242. (February 2010)
B. 4242. Is there an n, such that it is possible to walk the 4×n chessboard with a knight touching each field exactly once so that with a last step the knight returns to its original position? What happens if the knight is not required to return to the original position?
(4 pont)
Deadline expired on March 10, 2010.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Tegyük fel, hogy valamely \(\displaystyle n\)-re létezik egy ilyen bejárás, és rögzítsünk egy ilyet. Ekkor a szóban forgó \(\displaystyle 4\times n\)-es tábla minden mezőjének két szomszédja van: az egyik, ahonnan oda lépünk, a másik pedig ahová onnan lépünk; ezek az illető mezőtől eltérő sor(ok)ban helyezkednek el. A tábla mezőinek a sakktábláéhoz hasonló színezése mellett minden egyes mező szomszédai az adott mezőével ellentétes színűek. A két szélső sorban lévő \(\displaystyle 2n\) darab mező szomszédai mind a két középső sorba esnek, amivel mind a \(\displaystyle 4n\) szomszédságot át is tekintettük, vagyis a bejárás során nincsen olyan lépés, amely a két középső sor egyikéből a másikba történne. Ez azt jelenti, hogy minden második lépés után a huszár valamelyik szélső sorba, a többi lépés után pedig valamelyik középső sorba érkezik. Ennek megfelelően a bejárás során a huszár a szélső sorokban mindig ugyanolyan színű mezőre érkezik, a középső sorokban pedig azzal ellentétes színűre, ami nyilvánvaló ellentmondást jelent. Az első kérdésre tehát nemleges a válasz.
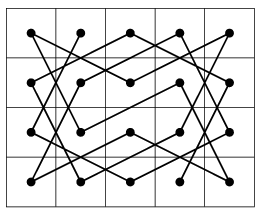
A második esetben viszont létezik ilyen \(\displaystyle n\), például \(\displaystyle n=5\). A \(\displaystyle 4\times 5\)-ös tábla lehetséges bejárását mutatja az alábbi ábra, melynek megtalálásában segíthet az előző gondolatmenet megfelelő módosítása.
Statistics:
42 students sent a solution. 4 points: Ágoston Péter, Cséke Balázs, Damásdi Gábor, Éles András, Gyarmati Máté, Halász Dániel, Hegedűs Csaba, Janzer Olivér, Karkus Zsuzsa, Kiss 902 Melinda Flóra, Korondi Zénó, Márkus Bence, Máthé László, Mester Márton, Mészáros András, Nagy 111 Miklós, Perjési Gábor, Réti Dávid, Szabó 928 Attila, Varnyú József, Zelena Réka. 3 points: Bogár Blanka, Janosov Milán, Kovács 235 Gábor, Repka 666 Dániel. 1 point: 15 students. 0 point: 2 students.
Problems in Mathematics of KöMaL, February 2010
