 Problem B. 4244. (February 2010)
Problem B. 4244. (February 2010)
B. 4244. Given the hypotenuse of a right-angled triangle and the radius of the excircle drawn to one of the legs, construct the triangle.
(4 pont)
Deadline expired on March 10, 2010.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A szerkesztendő \(\displaystyle ABC\) háromszög befogói legyenek \(\displaystyle AC=b\) és \(\displaystyle BC=a\), és tegyük fel, hogy a \(\displaystyle c\) átfogón kívül a \(\displaystyle BC\) oldalhoz hozzáírt kör \(\displaystyle r_a\) sugara adott. Az érintőszakaszok egyenlőségéből \(\displaystyle a+b+c=2(r_a+b)\), vagyis \(\displaystyle a-b=2r_a-c\) következik.
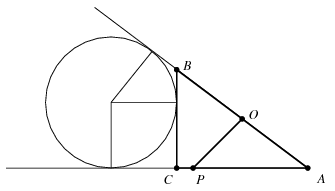
Mivel az \(\displaystyle AB\) átfogó \(\displaystyle O\) felezőpontja, ami az \(\displaystyle AC\) oldaltól \(\displaystyle a/2\), a \(\displaystyle BC\) oldaltól \(\displaystyle b/2\) távolságra helyezkedik el, éppen az \(\displaystyle ABC\) háromszög köré írható kör középpontja, \(\displaystyle OC=c/2\), és az \(\displaystyle O\) ponton át az ábra szerint az \(\displaystyle AC\) egyenessel \(\displaystyle 45^\circ\)-os szöget bezáró egyenes az \(\displaystyle AC\) egyenest abban a \(\displaystyle P\) pontban metszi, amelyre \(\displaystyle CP=|b/2-a/2|=|r_a-c/2|\). Ha \(\displaystyle r_a<c/2\), akkor ez \(\displaystyle P\) pont az \(\displaystyle AC\) befogón helyezkedik el, \(\displaystyle r_a=c/2\) esetén egybeesik \(\displaystyle C\)-vel, \(\displaystyle r_a>c/2\) esetén pedig a \(\displaystyle C\) pont másik oldalán helyezkedik el.
Ezek alapján a keresett háromszög a következő módon szerkeszthető meg. A leendő \(\displaystyle AC\) oldal egyenesén felvesszük a \(\displaystyle C\) pontot, és kijelöljük a \(\displaystyle CA\) félegyenes irányát, majd az előbbieknek megfelelően kijelöljük a \(\displaystyle P\) pontot is. Az egyenes egyik oldalán \(\displaystyle C\) középponttal \(\displaystyle c/2\) sugarú félkörívet rajzolunk. A \(\displaystyle P\) ponton át ugyanarra az oldalra az \(\displaystyle AC\) félegyenessel \(\displaystyle 45^\circ\)-os szöget bezáró félegyenest állítunk. Az \(\displaystyle O\) pontot a félegyenes és a félkör metszéspontjaként kapjuk. Végül az \(\displaystyle O\) középpontú \(\displaystyle c/2\) sugarú kör segítségével a \(\displaystyle CA\) egyenesből, illetve az arra \(\displaystyle C\)-ben állított merőlegesből kimetsszük az \(\displaystyle A\) és \(\displaystyle B\) pontokat.
Nem nehéz ellenőrizni, hogy a fenti szerkesztési eljárás pontosan akkor vezet, méghozzá egyértelmű eredményre, ha \(\displaystyle r_a<c\), és ekkor valóban a feladat megoldását szolgáltatja.
Statistics:
92 students sent a solution. 4 points: Ágoston Péter, Ágoston Tamás, Bálint Csaba, Böőr Katalin, Bősze Zsuzsanna, Csuka Róbert, Czipó Bence, Dolgos Tamás, Éles András, Gyarmati Máté, Janzer Olivér, Kovács 444 Áron, Márkus Bence, Medek Ákos, Mester Márton, Mihálka Éva Zsuzsanna, Neukirchner Elisabeth, Remete László, Somogyi Ákos, Tóth 222 Barnabás, Weimann Richárd, Weisz Ágoston, Zelena Réka. 3 points: 47 students. 2 points: 9 students. 1 point: 5 students. 0 point: 6 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, February 2010
