 |
A B. 4256. feladat (2010. március) |
B. 4256. Van-e olyan háromszög, melynek egyik szögét négy egyenlő részre osztja a szög csúcsán átmenő magasságvonal, súlyvonal és szögfelező?
(4 pont)
A beküldési határidő 2010. április 12-én LEJÁRT.
Megoldás. Tegyük fel, hogy az \(\displaystyle ABC\) háromszög \(\displaystyle C\)-nél lévő \(\displaystyle 4\alpha\) nagyságú szögét az ábra szerint négy egyenlő részre osztja az egység hosszúságú \(\displaystyle CH\) magasságvonal, a \(\displaystyle CF\) súlyvonal és a \(\displaystyle CG\) szögfelező, nyilván ez utóbbi van középen, és \(\displaystyle \alpha< 30^\circ\).
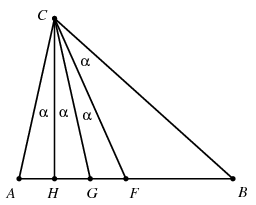
Ekkor \(\displaystyle AH=\tg\alpha\), \(\displaystyle FH=\tg2\alpha\), \(\displaystyle BH=\tg3\alpha\), vagyis
\(\displaystyle \tg\alpha+\tg2\alpha=AH+FH=FA=FB=BH-FH=\tg3\alpha-\tg2\alpha.\)
Az innen kapott \(\displaystyle \tg\alpha+\tg2\alpha=\tg3\alpha-\tg2\alpha\) feltétel szükséges, de egyben elegendő is: ha egy ennek eleget tevő \(\displaystyle \alpha<30^\circ\) szöggel a fenti ábrát megrajzoljuk, az így kapott \(\displaystyle ABC\) háromszögben \(\displaystyle CH, CF\) és \(\displaystyle CG\) éppen a \(\displaystyle C\)-ből induló magasságvonal, súlyvonal, illetve szögfelező lesz.
A \(\displaystyle 0<z=\tg\alpha<1/\sqrt{3}\) jelöléssel a tangens függvény addíciós képletét alkalmazva
\(\displaystyle \tg2\alpha=\frac{2z}{1-z^2},\qquad \tg3\alpha=\frac{\tg\alpha+\tg2\alpha}{1-\tg\alpha\tg2\alpha}=\frac{3z-z^3}{1-3z^2},\)
ahol a nevezőkben pozitív számok állnak. A \(\displaystyle \tg3\alpha=\tg\alpha+2\tg2\alpha\) egyenlőséget ennek megfelelően
\(\displaystyle \frac{3z-z^3}{1-3z^2}=z+\frac{4z}{1-z^2}\)
alakra hozhatjuk. Az egyenletet a nevezőkkel felszorozva \(\displaystyle z\)-re a
\(\displaystyle (3z-z^3)(1-z^2)=(5z-z^3)(1-3z^2)\)
összefüggést kapjuk, ami a \(\displaystyle z\ne 0\) számmal leosztva a \(\displaystyle 0<t=z^2<1/3\) helyettesítéssel a \(\displaystyle (3-t)(1-t)=(5-t)(1-3t)\) egyenlőséggel ekvivalens. Az innen nyert \(\displaystyle t^2-6t+1=0\) másodfokú egyenlet egyik megoldása \(\displaystyle t=3+\sqrt{8}\), ami nem jöhet szóba, a szintén pozitív \(\displaystyle t=3-\sqrt{8}\) megoldás viszont kisebb, mint \(\displaystyle 1/3\), az ennek megfelelő \(\displaystyle \alpha=\arctg\sqrt{3-\sqrt{8}}\) szög tehát kisebb, mint \(\displaystyle 30^\circ\), vagyis a feladat feltételeinek eleget tevő háromszöget szolgáltat.
Statisztika:
96 dolgozat érkezett. 4 pontot kapott: Ádám Liliána, Ágoston Péter, Ágoston Tamás, Bálint Csaba, Barczel Nikolett, Béres Ferenc, Boér Lehel, Bogár Blanka, Böőr Katalin, Cséke Balázs, Csere Kálmán, Csizmadia Luca, Dunay Luca, Énekes Péter, Gyarmati Máté, Hegedűs Csaba, Horváth 396 Dániel, Hosszejni Darjus, Jernei Tamás, Karkus Zsuzsa, Keresztfalvi Tibor, Klincsik Gergely, Korondi Zénó, Máthé László, Mester Márton, Mihálka Éva Zsuzsanna, Nagy Balázs, Nagy Róbert, Németh Bence, Nguyen Milán, Ódor Gergely, Popper Dávid, Rábai Domonkos, Sieben Bertilla, Somogyi Ákos, Tekeli Tamás, Tossenberger Tamás, Tóth 222 Barnabás, Tóth Tekla, Uray Marcell János, Varga Vajk, Varju 105 Tamás, Virágh Eszter, Weimann Richárd, Weisz Gellért, Zahemszky Péter, Zsakó András. 3 pontot kapott: 35 versenyző. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 5 versenyző. Nem versenyszerű: 3 dolgozat.
A KöMaL 2010. márciusi matematika feladatai

