 Problem B. 4259. (March 2010)
Problem B. 4259. (March 2010)
B. 4259. A circle passes through vertices B and C of a triangle ABC. It intersects side AB at D and side AC at E. The median AF intersects DE at G. Prove that .
(4 pont)
Deadline expired on April 12, 2010.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Mivel a \(\displaystyle BCED\) négyszög húrnégyszög, a szokásos jelölésekkel
\(\displaystyle AED\sphericalangle=180^\circ-CED\sphericalangle=CBD\sphericalangle=\beta,\)
és hasonlóképpen \(\displaystyle ADE\sphericalangle=\gamma\), vagyis az \(\displaystyle AED\) háromszög hasonló az \(\displaystyle ABC\) háromszöghöz. Húzzunk az \(\displaystyle F\) ponton át párhuzamost a \(\displaystyle DE\) egyenessel, ennek az \(\displaystyle AB\), illetve \(\displaystyle AC\) félegyenessel való metszéspontját jelölje \(\displaystyle D'\) és \(\displaystyle E'\). Ekkor az \(\displaystyle AE'D'\) háromszög hasonló az \(\displaystyle AED\) háromszöghöz, és \(\displaystyle GD:GE=FD':FE'\).
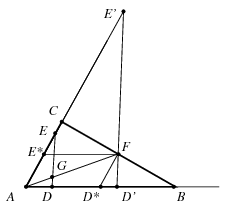
Ha az \(\displaystyle AB\) és \(\displaystyle AC\) oldalak felezőpontját \(\displaystyle D^*\), illetve \(\displaystyle E^*\) jelöli, akkor \(\displaystyle FD^*=AC/2\), \(\displaystyle FE^*=AB/2\), vagyis az \(\displaystyle ABC\), \(\displaystyle AED\), \(\displaystyle AE'D'\), \(\displaystyle E^*E'F\) és \(\displaystyle D^*FD'\) háromszögek hasonlósága alapján
\(\displaystyle \frac{GD}{GE}=\frac{FD'}{FE'}=\frac{FD'}{FD^*}\cdot\frac{FD^*}{FE^*}\cdot \frac{FE^*}{FE'}=\frac{BC}{AB}\cdot\frac{AC}{AB}\cdot\frac{CA}{CB}= \frac{AC^2}{AB^2}.\)
Statistics:
59 students sent a solution. 4 points: 53 students. 3 points: 2 students. 2 points: 1 student. 1 point: 1 student. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, March 2010
