 Problem B. 4269. (April 2010)
Problem B. 4269. (April 2010)
B. 4269. Construct the point P on side AB of triangle ABC for which the radii of the inscribed circles of triangles BCP and ACP are equal.
(5 pont)
Deadline expired on May 10, 2010.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Tekintsük a \(\displaystyle P\) pontot megszerkesztettnek. A két kör középpontját jelölje \(\displaystyle O_A\), illetve \(\displaystyle O_B\), a beírt kör középpontját \(\displaystyle O\). Ekkor \(\displaystyle O_A\) az \(\displaystyle AO\), \(\displaystyle O_B\) pedig a \(\displaystyle BO\) szakasz belső pontja, hiszen az \(\displaystyle A,O_A,O\) pontok az \(\displaystyle A\)-ból induló, a \(\displaystyle B,O_B,O\) pontok pedig a \(\displaystyle B\)-ből induló szögfelezőn helyezkednek el. Ha a két kis kör sugara egyenlő, akkor tehát az \(\displaystyle OO_AO_B\) háromszög hasonló az \(\displaystyle OAB\) háromszöghöz, a hasonlóság aránya pedig \(\displaystyle 1-\frac{r}{R}\), ahol \(\displaystyle R\) a beírt kör, \(\displaystyle r\) pedig a kis körök sugarát jelöli.
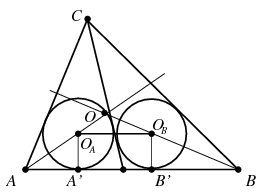
Az \(\displaystyle O_A,O_B\) pontok merőleges vetülete az \(\displaystyle AB\) oldalra legyen \(\displaystyle A'\), illetve \(\displaystyle B'\). A szokásos \(\displaystyle AB=c\), \(\displaystyle AC=b\), \(\displaystyle BC=a\) jelölések mellett legyen \(\displaystyle CP=f\), \(\displaystyle AP=c_A\), \(\displaystyle BP=c_B\), ekkor \(\displaystyle c_A+c_B=c\). Az \(\displaystyle ABC\), \(\displaystyle APC\) és \(\displaystyle BPC\) háromszögek kerületének felét jelölje \(\displaystyle s,s_A,s_B\). Ekkor
\(\displaystyle AA'=s_A-f=\frac{1}{2}(b+c_A-f),\quad BB'=s_B-f=\frac{1}{2}(a+c_B-f),\)
vagyis
\(\displaystyle O_AO_B=A'B'=c-AA'-BB'=c-\frac{1}{2}(a+b+c_A+c_B-2f)=f-s+c.\)
Mindezek alapján
\(\displaystyle 1-\frac{r}{R}=\frac{O_AO_B}{AB}=\frac{f-s+c}{c}=1-\frac{s-f}{c}.\)
A háromszög \(\displaystyle t\) területe a két kis háromszög területének összege, vagyis \(\displaystyle Rs=t=rs_A+rs_B=r(s+f)\), ahonnan
\(\displaystyle \frac{s-f}{c}=\frac{r}{R}=\frac{s}{s+f},\)
vagyis \(\displaystyle s^2-f^2=sc\), \(\displaystyle f^2=s(s-c)\), \(\displaystyle f=\sqrt{s(s-c)}\), ami a magasságtétel alapján a szokásos módon megszerkeszthető (mértani középarányos szerkesztése).
Ha tehát egyáltalán létezik a feltételnek eleget tevő \(\displaystyle P\) pont, akkor azt \(\displaystyle C\) középpontú \(\displaystyle f\) sugarú kör metszi ki az \(\displaystyle AB\) szakaszból. Ilyen \(\displaystyle P\) pont valóban létezik. Ha ugyanis a \(\displaystyle P\) pont befutja az \(\displaystyle AB\) szakaszt, akkor az \(\displaystyle ACP\) háromszögbe írható kör sugara 0 és \(\displaystyle R\), a \(\displaystyle BCP\) háromszögbe írható kör sugara pedig \(\displaystyle R\) és 0 között változik folytonos módon, vagyis kell lennie olyan helyzetnek, amelyben a két kör sugara egyenlő. Ilyen helyzetben vizsgálva az \(\displaystyle ACP\) és \(\displaystyle BCP\) háromszögek területének arányát, kapjuk, hogy
\(\displaystyle \frac{c_A}{c_B}=\frac{rs_A}{rs_B}=\frac{f+b+c_A}{f+a+c_B},\quad \hbox{vagyis}\quad \frac{c_A}{c_B}=\frac{f+b}{f+a},\)
a \(\displaystyle P\) pont helyzete tehát egyértelműen meghatározott. Az \(\displaystyle a\ge b\) feltevés mellett így
\(\displaystyle \frac{c_A}{c_B}=\frac{f+b}{f+a}\ge \frac{b}{a},\)
ami a szögfelező tétel értelmében azt jelenti, hogy a \(\displaystyle P\) pont a \(\displaystyle C\)-ből induló szögfelezőnek ugyanarra az oldalára esik, mint a \(\displaystyle B\) csúcs. Minthogy ebben az esetben a \(\displaystyle C\)-ből induló magasságvonal éppen a másik oldalra esik, a megoldást a fent említett körvonalnak és az \(\displaystyle AB\) egyenesnek \(\displaystyle B\)-hez közelebbi metszéspontja szolgáltatja, \(\displaystyle a=b\) esetén ez ugyan érintési pont lesz, de nyilván megegyezik az \(\displaystyle AB\) szakasz felezőpontjával. Ha pedig \(\displaystyle a<b\), akkor az \(\displaystyle A\)-hoz közelebbi metszéspontot kell venni.
Statistics:
22 students sent a solution. 5 points: Ágoston Tamás, Damásdi Gábor, Éles András, Janzer Olivér, Mester Márton, Nagy Balázs, Nagy Róbert, Perjési Gábor, Strenner Péter, Szabó 928 Attila, Weisz Ágoston, Weisz Gellért. 4 points: Dolgos Tamás, Gyarmati Máté, Kiss 902 Melinda Flóra, Somogyi Ákos, Szórádi Márk. 3 points: 2 students. 1 point: 1 student. 0 point: 2 students.
Problems in Mathematics of KöMaL, April 2010
