 |
A B. 4269. feladat (2010. április) |
B. 4269. Szerkesszük meg az ABC háromszög AB oldalán azt a P pontot, amelyre a BCP és ACP háromszögekbe írható körök sugara egyenlő.
(5 pont)
A beküldési határidő 2010. május 10-én LEJÁRT.
Megoldás. Tekintsük a \(\displaystyle P\) pontot megszerkesztettnek. A két kör középpontját jelölje \(\displaystyle O_A\), illetve \(\displaystyle O_B\), a beírt kör középpontját \(\displaystyle O\). Ekkor \(\displaystyle O_A\) az \(\displaystyle AO\), \(\displaystyle O_B\) pedig a \(\displaystyle BO\) szakasz belső pontja, hiszen az \(\displaystyle A,O_A,O\) pontok az \(\displaystyle A\)-ból induló, a \(\displaystyle B,O_B,O\) pontok pedig a \(\displaystyle B\)-ből induló szögfelezőn helyezkednek el. Ha a két kis kör sugara egyenlő, akkor tehát az \(\displaystyle OO_AO_B\) háromszög hasonló az \(\displaystyle OAB\) háromszöghöz, a hasonlóság aránya pedig \(\displaystyle 1-\frac{r}{R}\), ahol \(\displaystyle R\) a beírt kör, \(\displaystyle r\) pedig a kis körök sugarát jelöli.
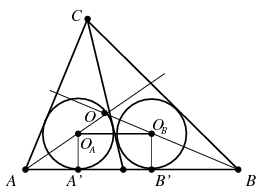
Az \(\displaystyle O_A,O_B\) pontok merőleges vetülete az \(\displaystyle AB\) oldalra legyen \(\displaystyle A'\), illetve \(\displaystyle B'\). A szokásos \(\displaystyle AB=c\), \(\displaystyle AC=b\), \(\displaystyle BC=a\) jelölések mellett legyen \(\displaystyle CP=f\), \(\displaystyle AP=c_A\), \(\displaystyle BP=c_B\), ekkor \(\displaystyle c_A+c_B=c\). Az \(\displaystyle ABC\), \(\displaystyle APC\) és \(\displaystyle BPC\) háromszögek kerületének felét jelölje \(\displaystyle s,s_A,s_B\). Ekkor
\(\displaystyle AA'=s_A-f=\frac{1}{2}(b+c_A-f),\quad BB'=s_B-f=\frac{1}{2}(a+c_B-f),\)
vagyis
\(\displaystyle O_AO_B=A'B'=c-AA'-BB'=c-\frac{1}{2}(a+b+c_A+c_B-2f)=f-s+c.\)
Mindezek alapján
\(\displaystyle 1-\frac{r}{R}=\frac{O_AO_B}{AB}=\frac{f-s+c}{c}=1-\frac{s-f}{c}.\)
A háromszög \(\displaystyle t\) területe a két kis háromszög területének összege, vagyis \(\displaystyle Rs=t=rs_A+rs_B=r(s+f)\), ahonnan
\(\displaystyle \frac{s-f}{c}=\frac{r}{R}=\frac{s}{s+f},\)
vagyis \(\displaystyle s^2-f^2=sc\), \(\displaystyle f^2=s(s-c)\), \(\displaystyle f=\sqrt{s(s-c)}\), ami a magasságtétel alapján a szokásos módon megszerkeszthető (mértani középarányos szerkesztése).
Ha tehát egyáltalán létezik a feltételnek eleget tevő \(\displaystyle P\) pont, akkor azt \(\displaystyle C\) középpontú \(\displaystyle f\) sugarú kör metszi ki az \(\displaystyle AB\) szakaszból. Ilyen \(\displaystyle P\) pont valóban létezik. Ha ugyanis a \(\displaystyle P\) pont befutja az \(\displaystyle AB\) szakaszt, akkor az \(\displaystyle ACP\) háromszögbe írható kör sugara 0 és \(\displaystyle R\), a \(\displaystyle BCP\) háromszögbe írható kör sugara pedig \(\displaystyle R\) és 0 között változik folytonos módon, vagyis kell lennie olyan helyzetnek, amelyben a két kör sugara egyenlő. Ilyen helyzetben vizsgálva az \(\displaystyle ACP\) és \(\displaystyle BCP\) háromszögek területének arányát, kapjuk, hogy
\(\displaystyle \frac{c_A}{c_B}=\frac{rs_A}{rs_B}=\frac{f+b+c_A}{f+a+c_B},\quad \hbox{vagyis}\quad \frac{c_A}{c_B}=\frac{f+b}{f+a},\)
a \(\displaystyle P\) pont helyzete tehát egyértelműen meghatározott. Az \(\displaystyle a\ge b\) feltevés mellett így
\(\displaystyle \frac{c_A}{c_B}=\frac{f+b}{f+a}\ge \frac{b}{a},\)
ami a szögfelező tétel értelmében azt jelenti, hogy a \(\displaystyle P\) pont a \(\displaystyle C\)-ből induló szögfelezőnek ugyanarra az oldalára esik, mint a \(\displaystyle B\) csúcs. Minthogy ebben az esetben a \(\displaystyle C\)-ből induló magasságvonal éppen a másik oldalra esik, a megoldást a fent említett körvonalnak és az \(\displaystyle AB\) egyenesnek \(\displaystyle B\)-hez közelebbi metszéspontja szolgáltatja, \(\displaystyle a=b\) esetén ez ugyan érintési pont lesz, de nyilván megegyezik az \(\displaystyle AB\) szakasz felezőpontjával. Ha pedig \(\displaystyle a<b\), akkor az \(\displaystyle A\)-hoz közelebbi metszéspontot kell venni.
Statisztika:
22 dolgozat érkezett. 5 pontot kapott: Ágoston Tamás, Damásdi Gábor, Éles András, Janzer Olivér, Mester Márton, Nagy Balázs, Nagy Róbert, Perjési Gábor, Strenner Péter, Szabó 928 Attila, Weisz Ágoston, Weisz Gellért. 4 pontot kapott: Dolgos Tamás, Gyarmati Máté, Kiss 902 Melinda Flóra, Somogyi Ákos, Szórádi Márk. 3 pontot kapott: 2 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2010. áprilisi matematika feladatai

