 Problem B. 4280. (May 2010)
Problem B. 4280. (May 2010)
B. 4280. M is the midpoint of the arc AB containing vertex C on the circumscribed circle k of triangle ABC. J is the centre of the escribed circle drawn to side AB. The perpendicular drawn to angle bisector CJ at point J intersects line AC at D and line BC at E. Line MJ intersects circle k again at F. Prove that the circle passing through points D, E, F touches the lines AC and BC, and also touches the circle k.
(5 pont)
Deadline expired on June 10, 2010.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A háromszög szögeit a szokásos módon \(\displaystyle \alpha, \beta, \gamma\)-val jelölve, a kerületi szögek tétele szerint \(\displaystyle AMB\angle =ACB\angle=\gamma\), így az \(\displaystyle AMB\) és \(\displaystyle CDE\) egyenlőszárú háromszögekben
\(\displaystyle MAB\angle=MBA\angle=CDE\angle=CED\angle=\frac{\pi-\gamma}{2}.\)
Ugyancsak a kerületi szögek tétele szerint \(\displaystyle MFA\angle=MBA\angle=MAB\angle=MFB\angle\), vagyis
\(\displaystyle AFJ\angle=\pi-AFM\angle=\pi-ADJ\angle=\pi-BEJ\angle=\pi-BFM\angle=BFJ\angle.\)
Ezek alapján az \(\displaystyle ADJF\) és a \(\displaystyle BEJF\) négyszög is húrnégyszög. Minthogy \(\displaystyle J\) az \(\displaystyle A\)-ból és \(\displaystyle B\)-ből induló külső szögfelezők metszéspontja,
\(\displaystyle JAD\angle=JAB\angle=\frac{\pi-\alpha}{2},\quad JBE\angle=JBA\angle=\frac{\pi-\beta}{2}.\)
Lévén \(\displaystyle \alpha+\beta+\gamma=\pi\), tudjuk, hogy
\(\displaystyle \frac{\pi-\alpha}{2}+\frac{\pi-\beta}{2}+\frac{\pi-\gamma}{2}=\pi.\)
Ezért az \(\displaystyle ADJ\), \(\displaystyle AJB\) és \(\displaystyle JEB\) háromszögek hasonlók, és
\(\displaystyle DJA\angle=\frac{\pi-\beta}{2}, \quad AJB\angle=\frac{\pi-\gamma}{2}, \quad EJB\angle=\frac{\pi-\alpha}{2}.\)
Kihasználva, hogy \(\displaystyle ADJF\) és \(\displaystyle BEJF\) húrnégyszög, \(\displaystyle FAD\angle=\pi-FJD\angle=FJE\angle\), továbbá
\(\displaystyle AFD\angle=AJD\angle=\frac{\pi-\beta}{2}=JBE\angle.\)
Ez azt jelenti, hogy az \(\displaystyle ADF\) és \(\displaystyle JEF\) háromszögek is hasonlók, vagyis \(\displaystyle ADF\angle=JEF\angle=DEF\angle\). Az \(\displaystyle ADF\) szög tehát megegyezik a \(\displaystyle DEF\) körben a \(\displaystyle DF\) húrhoz tartozó kerületi szöggel, vagyis az \(\displaystyle AD\) egyenes érinti a \(\displaystyle DEF\) kört. Ezzel beláttuk, hogy a \(\displaystyle DEF\) kör érinti az \(\displaystyle AC\) egyenest, és ugyanígy a \(\displaystyle BC\) egyenest is.
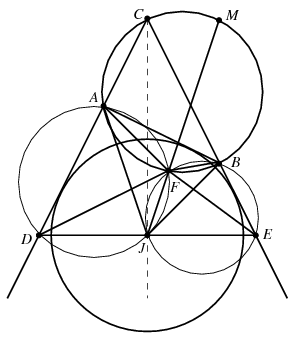
Húzzunk most képzeletben érintőt az \(\displaystyle ABC\) és a \(\displaystyle DEF\) körhöz is az \(\displaystyle F\) pontban. Előbbi a \(\displaystyle BF\) húrral \(\displaystyle BAF\), utóbbi az \(\displaystyle EF\) húrral \(\displaystyle EDF\) szöget zár be. Annak belátásához, hogy a két kör \(\displaystyle F\)-ben érinti egymást, elegendő megmutatni, hogy a két érintő egyenes egybeesik, vagyis hogy \(\displaystyle BFE\angle=BAF\angle+EDF\angle\). Ismét kihasználhatjuk, hogy \(\displaystyle ADJF\) és \(\displaystyle BEJF\) húrnégyszög és hogy az \(\displaystyle ADF\) és \(\displaystyle JEF\) háromszögek hasonlók. Ezek alapján
\(\displaystyle BAF\angle+EDF\angle=BAF\angle+JAF\angle=BAJ\angle=JAD\angle=BJE\angle=BFE\angle,\)
ahogy azt bizonyítani kívántuk.
Statistics:
10 students sent a solution. 5 points: Ágoston Tamás, Éles András, Márkus Bence, Mester Márton, Mészáros András, Perjési Gábor. 3 points: 2 students. 2 points: 1 student. 0 point: 1 student.
Problems in Mathematics of KöMaL, May 2010
