 Problem B. 4283. (September 2010)
Problem B. 4283. (September 2010)
B. 4283. A 23×23 square is divided into smaller squares of dimensions 1×1, 2×2 and 3×3. What is the minimum possible number of 1×1 squares?
(5 pont)
Deadline expired on October 11, 2010.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Legalább egy \(\displaystyle 1\times1\)-es négyzetre szükség van. Például:
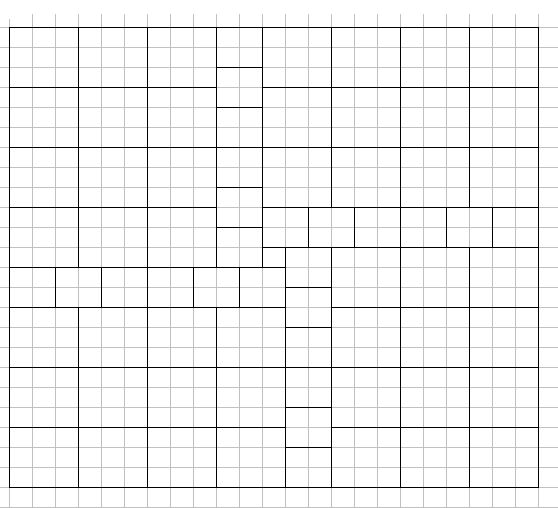
Ezután elegendő belátni, hogy \(\displaystyle 1\times1\)-es négyzet nélküli felbontás nem létezik.
Színezzük ki az 1., 4., 7., ..., 22. sorát szürkére a nagy négyzetnek:

Látható, hogy bárhogy teszünk le egy \(\displaystyle 2\times2\)-es vagy \(\displaystyle 3\times3\)-as négyzetet, mindig páros sok fehéren maradt mezőt fed le. De mivel \(\displaystyle 15\cdot23\), azaz páratlan számú fehéren maradt mező van, nem lehetséges, hogy csak \(\displaystyle 2\times2\)-es és \(\displaystyle 3\times3\)-as négyzetek fedjenek egy \(\displaystyle 23\times23\)-as négyzetet.
Tehát a válasz 1.
Damásdi Gábor (Kecskemét, Katona J. Gimn., 12. évf.)
Statistics:
143 students sent a solution. 5 points: Ágoston Péter, Beke Lilla, Bogár Blanka, Damásdi Gábor, Dobos Nóra, Dudás 002 Zsolt, Énekes Péter, Fonyó Viktória, Géczi Péter Attila, Gyarmati Máté, Hajnal Máté, Hajnal Péter János, Hegedűs Csaba, Herczeg József, Janzer Olivér, Kabos Eszter, Kaprinai Balázs, Kovács 737 Ármin, Köpenczei Gergő, Kúsz Ágnes, Lenger Dániel, Máthé László, Mátrahegyi Roland, Mihálykó András, Nagy 111 Miklós, Nagy Róbert, Németh Krisztián, Perjési Gábor, Sándor Áron Endre, Simig Dániel, Szabó 928 Attila, Tardos Jakab, Varga 149 Imre Károly, Varnyú József, Viharos Andor, Weisz Ambrus, Weisz Gellért, Zelena Réka, Zsiros Ádám. 4 points: Homonnay Bálint, Palincza Richárd, Strenner Péter, Tekeli Tamás, Wiandt Zsófia. 3 points: 6 students. 2 points: 28 students. 1 point: 2 students. 0 point: 62 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, September 2010
