Problem B. 4286. (September 2010)

B. 4286. The leg of an isosceles right angled triangle is 36 units long. Starting at the right-angled vertex on one of the legs, an infinite sequence of regular triangles is drawn. One side of each triangle lies on the leg and the third vertex lies on the hypotenuse. The sides on the leg link together and cover the whole leg. Find the total area of the regular triangles.

(Based on a Kavics Kupa competition problem)

(4 pont)

Deadline expired on October 11, 2010.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A derékszögű háromszög csúcsai legyenek az ábra szerint \(\displaystyle A,B,C\). Az \(\displaystyle AC\) befogóra rajzolt szabályos háromszögek közül a legnagyobbnak az egyik csúcsa \(\displaystyle C\) kell legyen, ez a \(\displaystyle CDX\) háromszög a végtelen sorozat első eleme.

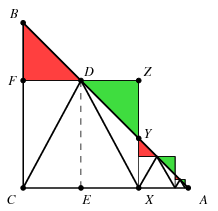
A \(\displaystyle D\) csúcs vetülete az \(\displaystyle AC,BC\) befogókra legyen \(\displaystyle E\), illetve \(\displaystyle F\), a \(\displaystyle DF\) egyenesre \(\displaystyle X\)-ben állított merőlegesnek az \(\displaystyle AB\) és \(\displaystyle DF\) egyenesekkel alkotott metszéspontja pedig \(\displaystyle Y\), illetve \(\displaystyle Z\). Mivel \(\displaystyle FD=CE=EX=DZ\), a \(\displaystyle BDF\) és \(\displaystyle YDZ\) egyenlő szárú derékszögű háromszögek egybevágók. Ezért a \(\displaystyle BCXY\) trapéz területe megegyezik az \(\displaystyle FCXZ\) téglalap területével, melynek pontosan a felét tölti ki a \(\displaystyle CDX\) háromszög.

Ha a végtelen sorozatban szereplő háromszögek \(\displaystyle AC\) befogóra eső csúcsaiban merőlegeseket állítunk az \(\displaystyle AC\) egyenesre, akkor ezek az \(\displaystyle ABC\) háromszöget a \(\displaystyle BCXY\) trapézhoz hasonló négyszögek végtelen sorozatára bontják úgy, hogy minden egyes háromszög az őt tartalmazó trapéz területének pontosan felét tölti ki. Ezért a szabályos háromszögek területének összege megegyezik az \(\displaystyle ABC\) háromszög területének felével, ami \(\displaystyle 36^2/4=18^2=324\) területegységet tesz ki.

Statistics:

151 students sent a solution.
4 points:	85 students.
3 points:	39 students.
2 points:	10 students.
1 point:	2 students.
0 point:	11 students.
Unfair, not evaluated:	4 solutionss.

Problems in Mathematics of KöMaL, September 2010