 Problem B. 4292. (October 2010)
Problem B. 4292. (October 2010)
B. 4292. The feet of the perpendiculars dropped from vertex C of triangle ABC onto the interior angle bisectors from vertices A and B are E and F, respectively. The inscribed circle of the triangle touches side AC at point D. Prove that EF=CD.
(3 pont)
Deadline expired on November 10, 2010.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A szögfelezők a háromszögbe írható kör \(\displaystyle O\) középpontjában metszik egymást. Az \(\displaystyle AOB\), \(\displaystyle BOC\), \(\displaystyle COA\) szögek nagysága rendre
\(\displaystyle \pi-\frac{\alpha}{2}-\frac{\beta}{2}=\frac{\pi+\gamma}{2},\ \frac{\pi+\alpha}{2},\ \frac{\pi+\beta}{2}.\)
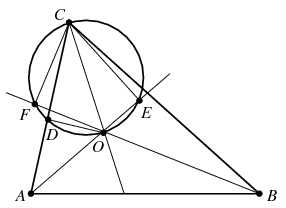
Ezért \(\displaystyle COE\) és \(\displaystyle COF\) szög is hegyesszög, továbbá
\(\displaystyle EOF\sphericalangle=AOB\sphericalangle=\frac{\pi+\gamma}{2}\)
és
\(\displaystyle COD\sphericalangle=\frac{\pi-\gamma}{2}=\pi-EOF\sphericalangle=ECF\sphericalangle.\)
Mivel a \(\displaystyle CDO, CEO\) és \(\displaystyle CFO\) szög is derékszög, a \(\displaystyle D,E,F\) pontok a \(\displaystyle CO\) átmérőjű körön helyezkednek el. Ebben a körben a \(\displaystyle CD\) és \(\displaystyle EF\) húrhoz egyaránt \(\displaystyle \frac{\pi-\gamma}{2}\) nagyságú kerületi szög tartozik, vagyis a két húr valóban ugyanolyan hosszú.
Statistics:
90 students sent a solution. 3 points: 60 students. 2 points: 22 students. 1 point: 3 students. 0 point: 4 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, October 2010
