 Problem B. 4303. (November 2010)
Problem B. 4303. (November 2010)
B. 4303. A rectangle that is not a square is folded in two along a diagonal. Prove that the perimeter of the resulting pentagon is smaller than the perimeter of the original rectangle.
(3 pont)
Deadline expired on December 10, 2010.
Sorry, the solution is available only in Hungarian. Google translation
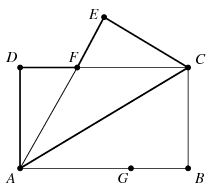
Megoldás. Tegyük fel, hogy az \(\displaystyle ABCD\) téglalapban \(\displaystyle AB>AD\), és a téglalapot az \(\displaystyle AC\) átlója mentén hajtjuk félbe úgy, hogy a \(\displaystyle B\) pont az \(\displaystyle E\) pontba kerül. Az \(\displaystyle AE\) és \(\displaystyle CD\) szakaszok metszéspontja legyen \(\displaystyle F\). Legyen továbbá \(\displaystyle G\) az \(\displaystyle AB\) oldal azon pontja, amelyre \(\displaystyle AF=AG\). Mivel \(\displaystyle BC=CE\) és \(\displaystyle GB=FE\), a félbehajtás során a kerület csökken az \(\displaystyle AG+FC=AF+FC\) mennyiséggel, ugyanakkor növekszik az \(\displaystyle AC\) mennyiséggel. A háromszög-egyenlőtlenség miatt \(\displaystyle AC<AF+FC\), ezért a kerület összességében csökken.
Statistics:
231 students sent a solution. 3 points: 114 students. 2 points: 69 students. 1 point: 21 students. 0 point: 19 students. Unfair, not evaluated: 8 solutionss.
Problems in Mathematics of KöMaL, November 2010
