Problem B. 4305. (November 2010)

B. 4305. What is the largest possible number of edges of a pyramid with an n-sided base that a plane may intersect?

(4 pont)

Deadline expired on December 10, 2010.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Tegyük fel, hogy a sík az alaplapnak \(\displaystyle e\) elét metszi, méghozzá úgy, hogy az alaplapnak \(\displaystyle a\) csúcsa esik a sík egyik oldalára, \(\displaystyle b\) a másikra, ahol \(\displaystyle a\le b\) és \(\displaystyle a+b\le n\). Az \(\displaystyle e\) él mindegyikének van csúcsa a sík mindkét oldalán. Mivel az \(\displaystyle e\) él közül az \(\displaystyle a\) csúcs mindegyikére legfeljebb kettő illeszkedik, \(\displaystyle e\le 2a\). A sík ezen felül \(\displaystyle 0\), \(\displaystyle a\) vagy \(\displaystyle b\) oldalélet metsz, attól függően, hogy a gúla csúcsa a sík melyik oldalára esik. A sík tehát a gúlának legfeljebb

\(\displaystyle 2a+b\le n+a\le \lfloor \frac{3n}{2}\rfloor\)

élét metszheti.

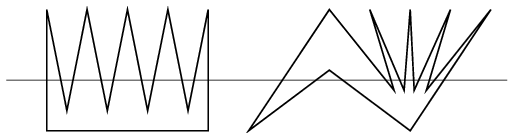
Ez el is érhető. A fenti gondolatmenetből ugyanis látszik, hogy ehhez elegendő találni olyan \(\displaystyle n\) oldalú sokszöget, melyhez létezik olyan egyenes, amely a sokszögnek \(\displaystyle n\), illetve \(\displaystyle n-1\) élét metszi, attól függően, hogy \(\displaystyle n\) páros avagy páratlan. Ilyen sokszögek konstrukcióját mutatja a fenti ábra; a részleteket az olvasó könnyen kidolgozhatja.

Statistics:

119 students sent a solution.
4 points:	Ágoston Péter, Beleznay Soma, Herczeg József, Kiss 542 Robin, Lenger Dániel, Perjési Gábor, Sieben Bertilla, Simig Dániel, Veitz Kristóf Tamás, Viharos Andor.
3 points:	Bogár Blanka, Böőr Katalin, Bunth Gergely, Damásdi Gábor, Dankovics Viktor, Kapronczay Mór, Kovács 737 Ármin, Medek Ákos, Nagy 224 Réka, Nagy Péter Áron, Sándor Áron Endre, Schultz Vera Magdolna, Szilágyi Gergely Bence, Varnyú József, Weimann Richárd.
2 points:	7 students.
1 point:	5 students.
0 point:	81 students.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, November 2010