Problem B. 4307. (November 2010)

B. 4307. Given two points on each of two sides of triangle ABC, prove that at least one of the four triangles formed by the four points has an area that is not greater than one quarter of the area of triangle ABC.

(L. Surányi, Budapest)

(4 pont)

Deadline expired on December 10, 2010.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A háromszög területe legyen egységnyi, a négy pontot pedig jelölje \(\displaystyle P,Q,R,S\) az ábra szerint. Legyen továbbá \(\displaystyle CP=\alpha\cdot AC\), \(\displaystyle CR=\beta\cdot BC\), ahol \(\displaystyle 0<\alpha,\beta <1\). Ekkor \(\displaystyle PQ=\gamma\cdot AC\) és \(\displaystyle RS=\delta\cdot BC\), ahol \(\displaystyle 0<\gamma\le 1-\alpha\) és \(\displaystyle 0<\delta\le 1-\beta\).

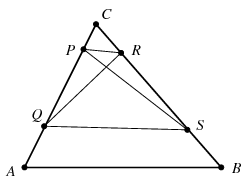
A \(\displaystyle PQR\) háromszög területe \(\displaystyle \beta\gamma\), az \(\displaystyle RSP\) háromszögé \(\displaystyle \alpha\delta\). Elég megmutatni, hogy valamelyik nem nagyobb 1/4-nél. Ha mindkettő nagyobb lenne, mint 1/4, akkor

\(\displaystyle 1=\frac{\alpha+(1-\beta)}{2}+\frac{\beta+(1-\alpha)}{2}\ge \sqrt{\alpha(1-\beta)}+\sqrt{\beta(1-\alpha)}\ge \sqrt{\alpha\delta}+\sqrt{\beta\gamma}>\frac{1}{2}+\frac{1}{2}=1\)

lenne, ami ellentmondás. Ha a \(\displaystyle P\) és \(\displaystyle R\) pontokat az \(\displaystyle AC\), illetve \(\displaystyle BC\) oldalak felezőpontjának választjuk, továbbá \(\displaystyle Q=A\) és \(\displaystyle S=B\), akkor látható az is, hogy a feladat állítása éles.

Statistics:

53 students sent a solution.
4 points:	Beleznay Soma, Bogár Blanka, Bunth Gergely, Czipó Bence, Damásdi Gábor, Dolgos Tamás, Énekes Péter, Fonyó Viktória, Gyarmati Máté, Győrfi 946 Mónika, Homonnay Bálint, Kabos Eszter, Karl E. Holter, Köpenczei Gergő, Lajos Mátyás, Machó Bónis, Medek Ákos, Mihálykó András, Nagy Róbert, Perjési Gábor, Peszt Anna, Schultz Vera Magdolna, Sieben Bertilla, Simig Dániel, Strenner Péter, Tatár Dániel, Tossenberger Tamás, Varnyú József, Veitz Kristóf Tamás, Viharos Andor, Weimann Richárd, Weisz Gellért, Zilahi Tamás, Zsakó András.
3 points:	Ágoston Péter, Dinev Georgi, Dudás 002 Zsolt, Kenéz Balázs, Kiss 542 Robin, Lenger Dániel, Maga Balázs, Solti Bálint, Szabó 928 Attila, Tulassay Zsolt, Vajda Balázs.
2 points:	2 students.
1 point:	4 students.
0 point:	2 students.

Problems in Mathematics of KöMaL, November 2010