Problem B. 4314. (December 2010)

B. 4314. The radii of three concentric circles are 1, 2, and 3 units. A point is marked on each circle such that they form a regular triangle. What may be the length of the side of the triangle?

(4 pont)

Deadline expired on January 10, 2011.

Sorry, the solution is available only in Hungarian. Google translation

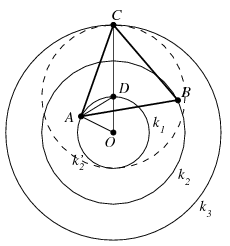
Megoldás. A körök legyenek rendre \(\displaystyle k_1\), \(\displaystyle k_2\), \(\displaystyle k_3\), a három kiválasztott pontot jelölje rendre \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\), a körök közös középpontját pedig \(\displaystyle O\). Tekintsük azt az \(\displaystyle A\) körüli \(\displaystyle 60^\circ\)-os forgatást, amely a \(\displaystyle B\) pontot \(\displaystyle C\)-be viszi; ez az \(\displaystyle O\) pontot a \(\displaystyle k_1\) kör egy \(\displaystyle D\) pontjába viszi. A \(\displaystyle k_2\) kör \(\displaystyle k_2'\) képe tehát egy \(\displaystyle D\) középpontú 2 sugarú körvonal, amely áthalad a \(\displaystyle C\) ponton. Ez a \(\displaystyle C\) pont a \(\displaystyle k_2'\)-t érintő \(\displaystyle k_3\) körre is illeszkedik, tehát \(\displaystyle C\)-ben ennek a két körnek közös érintője van. Ez azt jelenti, hogy a \(\displaystyle D\) pont illeszkedik az \(\displaystyle OC\) szakaszra, vagyis a \(\displaystyle COA\) szög megegyezik a \(\displaystyle 60^\circ\)-os \(\displaystyle DOA\) szöggel. A \(\displaystyle COA\) háromszögben \(\displaystyle OC=3\) és \(\displaystyle OA=1\), vagyis a koszinusz tétel szerint a szabályos háromszög oldala

\(\displaystyle AC=\sqrt{OC^2+OA^2-2\cdot OC\cdot OA\cdot\cos60^\circ}=\sqrt{7}.\)

A megoldásból könnyen látható az is, hogy ilyen háromszög valóban létezik.

Statistics:

80 students sent a solution.
4 points:	52 students.
3 points:	4 students.
2 points:	4 students.
1 point:	2 students.
0 point:	17 students.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, December 2010