B. 4318. Let P and Q be arbitrary points on the edges AB and CD of a given tetrahedron ABCD, respectively. Determine the locus of the midpoint of the line segment PQ.

(4 points)

Deadline expired.

Sorry, the solution is published in Hungarian only.

Az AC,BC,BD,AD élek felezőpontjai legyenek rendre X,Y,Z,V. Ekkor XY és ZV is párhuzamos az AB éllel, és fele olyan hosszú, vagyis az XY és ZV szakaszok egyenlő hosszúak és párhuzamosak egymással. Hasonló állítás érvényes az YZ és VX szakaszokra is, tehát ilyen módon egy XYZV paralelogramma jön létre. állítjuk, hogy ennek a paralolagrammának a pontjai alkotják a keresett mértani helyet.

Legyen P az AB él egy tetszőleges rögzített pontja, és tegyük fel, hogy P az AB szakaszt :(1-) arányban osztja. Ekkor a CP szakasz P' felezőpontja is :(1-) arányban osztja az XY szakaszt, valamint a DP szakasz P'' felezőpontja is :(1-) arányban osztja az VZ szakaszt. Itt P'P'' a CDP háromszög CD-vel párhuzamos középvonala, így miközben a Q pont befutja a CD élet, aközben a PQ szakasz felezőpontja éppen a P'P'' szakaszt futja be, amely része az XYZV paralelogrammának.

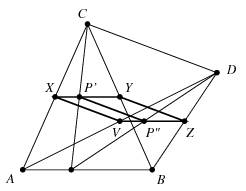
Látjuk tehát, hogy a mértani hely minden pontja az XYZV paralelogrammához tartozik. Mivel a paralelogramma minden, az XV oldallal párhuzamos metszete megkapható, mint P'P'' szakasz a P pont, vagyis a 01 szám megfelelő választása esetén, az is látszik, hogy a paralelogramma minden pontja a mértani helyhez tartozik.

Statistics on problem B. 4318. 74 students sent a solution. 4 points: Ágoston Péter, Bősze Zsuzsanna, Homonnay Bálint, Kiss 542 Robin, Máthé László, Sieben Bertilla, Simig Dániel, Strenner Péter, Varnyú József, Viharos Andor, Weimann Richárd. 3 points: Bálint Csaba, Beke Lilla, Csörgő András, Czipó Bence, Dinev Georgi, Dolgos Tamás, Győrfi 946 Mónika, Kabos Eszter, Kenéz Balázs, Lenger Dániel, Maga Balázs, Mátrahegyi Roland, Medek Ákos, Nagy 111 Miklós, Ódor Gergely, Tatár Dániel, Tossenberger Tamás, Weisz Gellért, Zilahi Tamás. 2 points: 17 students. 1 point: 14 students. 0 point: 12 students. Unfair, not evaluated: 1 solution.