 Problem B. 4322. (January 2011)
Problem B. 4322. (January 2011)
B. 4322. Five applicants are to be scheduled for job interviews at five given times. On an application form, each applicant was asked to mark two out of the five times. What is the probability that each of them can be interviewed at one of the two times they have marked?
(Suggested by G. Holló, Budapest)
(4 pont)
Deadline expired on February 10, 2011.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Ha \(\displaystyle n\ge 2\) embert szeretnének \(\displaystyle n\) előre adott lehetséges időpontra behívni úgy, hogy mindenki két lehetséges időpontot jelöl meg, akkor ennek szükséges feltétele, hogy minden \(\displaystyle k\le n\) esetén a jelentkezők közül bármely \(\displaystyle k\) ember együttesen legalább \(\displaystyle k\) időpontot megjelöljön. (Ez a feltétel egyben elégséges is, de erre a megoldás során nem lesz szükségünk). Készítsük el a következő páros gráfot. Az egyik színosztály csúcsai legyenek a jelentkezők, a másikéi az időpontok, és minden jelentkezőt kössünk össze az általa megjelölt két időponttal. Ennek a gráfnak 10 csúcsa és 10 éle van. Ha a gráf nem összefüggő, akkor a fenti feltétel szerint minden összefüggőségi komponense egy olyan páros gráf kell legyen, amelyben a két színosztály mérete ugyanakkora, az élek száma pedig megegyezik a csúcsok számával. Stratégiánk a következő lesz: először megvizsgáljuk, mely szóbajövő gráfok esetén létesíthető a színosztályok között a kívánt teljes párosítás, majd minden egyes ilyen gráfra leszámoljuk, hogy az \(\displaystyle {5\choose 2}^5=100000\) lehetőség között az adott gráf hányszor fordul elő.
Hasznos lesz a következő észrevétel. Ha egy \(\displaystyle n\) szögpontú gráf összefüggő, akkor legalább \(\displaystyle n-1\) éle van, és pontosan akkor nem tartalmaz kört, ha csak \(\displaystyle n-1\) éle van. Ebből következik, hogy ha a gráfnak \(\displaystyle n\) éle van, akkor pontosan egy kör lesz benne. Páros gráf esetén ennek a körnek a hossza páros, és található benne párosítás.
Mármost ha a választott időpontokhoz tartozó gráf nem összefüggő, akkor az egyik komponensének 4, a másiknak 6 csúcsa van. Tehát az első komponens egy 4 hosszú kör, a másik pedig vagy egy 6 hosszú kör, vagy tartalmaz egy 4 hosszú kört. Ez a kör mindkét színosztályból egy-egy csúcsot kihagy, melyeket egy él köt össze, ha a meghallgatás lehetséges. Az élnek az első színosztályba eső végpontja pedig össze van kötve a 4 hosszú kör másik színosztályba eső valamelyik csúcsával. Ezek alapján két különböző nem összefüggő gráf van, amely a feltételeket teljesíti, jelölje ezeket \(\displaystyle G_1\) és \(\displaystyle G_2\).
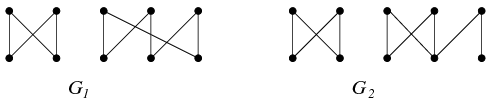
Ha a gráf összefüggő, akkor egy 10, egy 8, egy 6, vagy egy 4 hosszú kört tartalmaz. A 10 hosszú kör esetén meg is kaptuk az egész gráfot, ezt jelölje \(\displaystyle G_3\). Ha 8 hosszú körünk van, akkor ez mindkét színosztályból egy-egy csúcsot kihagy, melyek össze kell legyenek kötve egy éllel, hiszen a kör csúcsait egymás között kell párosítanunk, továbbá ennek az élnek az első színosztályba eső végpontja össze van kötve a 8 hosszú kör másik színosztályba eső valamelyik csúcsával. Így kapjuk a \(\displaystyle G_4\) gráfot. Ha 6 hosszú körünk van, akkor ez mindkét színosztályból két-két csúcsot hagy ki, melyek egymás között össze kell legyenek párosítva. Ebben a párosításban mindkét él első színosztályba eső végpontja össze van kötve a második színosztály valamelyik pontjával. Három esetet különböztethetünk meg, mivel legalább az egyiknek a 6 hosszú körhöz kell csatlakoznia. Ha pontosan az egyik csatlakozik a 6 hosszú körhöz, ahhor a \(\displaystyle G_5\) gráfot kapjuk, ha pedig mindkettő, akkor a \(\displaystyle G_6\), illetve a \(\displaystyle G_7\) gráfhoz jutunk aszerint, hogy a 6 hosszú körnek ugyanahhoz a csúcsához csatlakoznak, vagy sem.
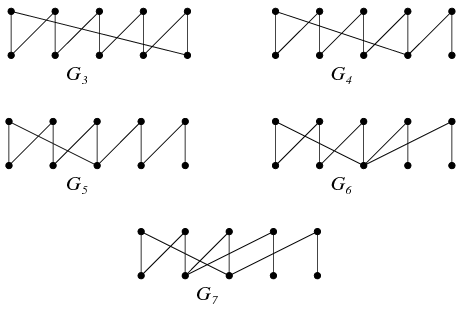
Végül ha 4 hosszú körünk van, akkor mindkét színosztályból három-három pont marad ki, melyek egymás között össze kell legyenek párosítva. Mivel legalább az egyik élnek a 4 hosszú körhöz kell csatlakozni, az alábbi hat gráfot kapjuk az eddigiek mellé.
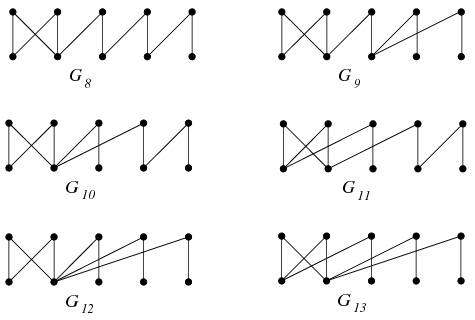
Jelölje \(\displaystyle a_i\) azon lehetőségek számát, amikor a \(\displaystyle G_i\) gráf jön létre. Ha a gráf nem összefüggő, akkor a 4 pontú komponens csúcsait bármelyik színosztályból \(\displaystyle {5\choose 2}=10\)-féleképpen választhatjuk ki, a 4 pont kiválasztása után rajtuk a 4 hosszú kör lerajzolása már egyértelmű. A \(\displaystyle G_1\) gráf esetében a fennmaradó 6 ponton a 6 hosszú kört 6-féleképpen tudjuk megrajzolni, a \(\displaystyle G_1\) gráf tehát \(\displaystyle a_1=10\times 10\times 6=600\) alkalommal jön létre. A \(\displaystyle G_2\) gráf esetében a 6-pontú komponensen a 4 hosszú kör kiválasztása \(\displaystyle {3\choose 2}^2=9\)-féleképpen történhet, az ettől diszjunkt él első színosztályba eső csúcsát ehhez kétféleképpen tudjuk csatlakoztatni. Így \(\displaystyle a_2=100\times 9\times 2=1800\). Ahhoz, hogy egy 10 hosszú kört rajzoljunk, induljunk el az első színosztály első csúcsából, ezt összeköthetjük a második színosztály bármelyik pontjával. Innen a kör 4-féleképpen folytatható, mert az első színosztályban már csak 4 csúcs maradt szabadon. Onnan megint 4-féleképpen folytathatjuk a kört a második színosztály fennmaradt pontjaival, de ezután már csak 3 lehetőség nyílik a folytatásra, és így tovább, a hetedik él behúzása után viszont már a befejezés egyértelmű lesz. Ez tehát \(\displaystyle 5\times 4\times 4\times 3\times 3\times 2\times 2=5\cdot(4!)^2=2880\) lehetőség. Viszont így mindegyik kört kétszer számoltuk, vagyis \(\displaystyle a_3=2880/2=1440\). A \(\displaystyle G_4\) gráf esetében a 8 hosszú kör csúcsainak kiválasztására \(\displaystyle 5\times 5=25\) lehetőségünk van, a kiválasztott pontokon a kör megrajzolása \(\displaystyle 4(3!)^2/2=72\)-féleképpen történhet. Ezután a körtől diszjunkt él első színosztályba eső csúcsát ehhez négyféleképpen tudjuk csatlakoztatni, vagyis \(\displaystyle a_4=25\times 72\times 4= 7200\). A \(\displaystyle G_5,G_6,G_7\) gráfok esetében a 6 hosszú kört \(\displaystyle 10\times 10\times 6=600\)-féleképpen vehetjük fel. A kimaradó 4 pont párosítása mindegyik esetben kétféleképp történhet, ami után a gráf befejezésére rendre 6, 3, illetve 6 lehetőség adó dik. Ezek szerint \(\displaystyle a_5=a_7=600\times 2\times 6=7200\), \(\displaystyle a_6=3600\). Végül a \(\displaystyle G_8-G_{13}\) gráfok esetében a 4 hosszú kör felvétele 100-féleképpen történhet, ezután a maradék 6 pont párosítására 6 lehetőségünk van, majd a befejezés rendre 12, 6, 12, 12, 2, illetve 6 különböző módon lehetséges. Ennek alapján \(\displaystyle a_8=a_{10}=a_{11}=7200\), \(\displaystyle a_{12}=1200\) és \(\displaystyle a_9=a_{13}=3600\).
Összefoglalva, a jelentkezők időpontmegjelölésének 100000 elképzelhető kimenetele közül \(\displaystyle a_1+\ldots+a_{13}=59040\) esetben tudnak mindenkit meghallgatni az egyik általa megjelölt időpontban. A keresett valószínűség tehát \(\displaystyle 0,5904\).
Statistics:
60 students sent a solution. 4 points: Bunth Gergely. 3 points: Homonnay Bálint. 2 points: 7 students. 1 point: 13 students. 0 point: 37 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, January 2011
