 Problem B. 4344. (March 2011)
Problem B. 4344. (March 2011)
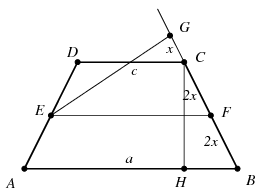
B. 4344. The lengths of the parallel sides of a symmetric trapezium are a and c. The midpoints of the legs are E and F. Let G denote the orthogonal projection of point E on the line of the leg BC. What is the area of the trapezium if point C divides the line segment GF in a 1:2 ratio? (C lies closer to point G.)
(4 pont)
Deadline expired on April 11, 2011.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A feladat szövege alapján világos, hogy az \(\displaystyle E\) és \(\displaystyle F\) pontok rendre az \(\displaystyle AD\), illetve a \(\displaystyle BC\) szár felezőpontjai, továbbá az \(\displaystyle AB\) alap hosszabb mint a \(\displaystyle CD\) alap. Ezek szerint \(\displaystyle a\ne c\). Tegyük fel, hogy \(\displaystyle a>c\). A szárak hossza legyen \(\displaystyle 4x\), ekkor \(\displaystyle FG=3x\). Ha a \(\displaystyle C\) csúcsnak az \(\displaystyle AB\) alapra eső merőleges vetülete \(\displaystyle H\), akkor \(\displaystyle EF=\frac{a+c}{2}\) és \(\displaystyle BH=\frac{a-c}{2}\). Az \(\displaystyle EFG\) és \(\displaystyle CBH\) derékszögű háromszögek hasonló volta miatt
\(\displaystyle 12x^2=CB\cdot FG=EF\cdot BH=\frac{a+c}{2}\cdot \frac{a-c}{2} =\frac{a^2-c^2}{4}.\)
Ezek alapján a trapéz területe
\(\displaystyle EF\cdot CH=EF\cdot\sqrt{CB^2-BH^2}= \frac{a+c}{2}\cdot \sqrt{(4x)^2-\left(\frac{a-c}{2}\right)^2}\)
\(\displaystyle =\frac{a+c}{2}\cdot \sqrt{\frac{a^2-c^2}{3}-\left(\frac{a-c}{2}\right)^2} =\frac{a+c}{2}\cdot \sqrt{\frac{a^2+6ac-7c^2}{12}}\)
\(\displaystyle =\sqrt{\frac{(a+c)^2(a+7c)(a-c)}{48}}.\)
Statistics:
87 students sent a solution. 4 points: 62 students. 3 points: 8 students. 2 points: 3 students. 1 point: 7 students. 0 point: 5 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, March 2011
