Problem B. 4352. (April 2011)

B. 4352. What is the minimum possible number of convex pentagons needed to put together a convex 2011-sided polygon out of them?

(Suggested by J. Mészáros, Jóka)

(3 pont)

Deadline expired on May 10, 2011.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Tegyük fel, hogy \(\displaystyle k\) darab konvex ötszögből sikerült összerakni egy konvex 2011-szöget. Ekkor a felhasznált ötszögek szögeinek összege, \(\displaystyle 3k\pi\), legalább akkora kell legyen, mint a 2011-szög szögeinek összege, ami \(\displaystyle 2011\pi -2\pi=2009\pi\). Ebből \(\displaystyle 3k\ge 2009\), vagyis \(\displaystyle k\ge 670\) következik, és az is látható, hogy kell legyen az ötszögek között legalább egy olyan, amelynek valamelyik csúcsa nem esik egybe a 2011-szög egyik csúcsával sem.

Másrészről 670 darab konvex ötszög elegendő is egy konvex 2011-szög összerakásához. Valóban, tetszőleges konvex 2011-szög felbontható 670 darab konvex ötszögre az alábbi eljárással. Először egy alkalmas átló segítségével bontsuk fel a sokszöget egy konvex hétszögre és egy konvex 2006-szögre. A hétszöget felbonthatjuk két darab ötszögre, ha egyik csúcsát összekötjük az azzal szemközti oldal egy belső pontjával. a nagyobbik sokszöget pedig felbonthatjuk 668 darab konvex ötszögre, ha valamelyik csúcsából berajzoljuk minden harmadik átlót.

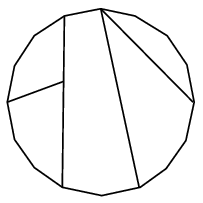
Ezzel a módszerrel valójában tetszőleges konvex \(\displaystyle (3n+1)\)-szöget \(\displaystyle n\) darab konvex ötszögre bonthatunk \(\displaystyle n\ge 2\) esetén; ábránk az eljárást \(\displaystyle n=5\) esetén szemlélteti.

Statistics:

73 students sent a solution.
3 points:	Balogh Adrienn Judit, Barczel Nikolett, Bősze Zsuzsanna, Bunth Gergely, Damásdi Gábor, Dudás 002 Zsolt, Emri Tamás, Énekes Péter, Énekes Tamás, Fonyó Viktória, Győrfi 946 Mónika, Janzer Barnabás, Kabos Eszter, Kenéz Balázs, Medek Ákos, Molnár Ákos, Schultz Vera Magdolna, Szabó 928 Attila, Tatár Dániel, Viharos Andor, Zelena Réka.
2 points:	Ágoston Péter, Balázs Bálint, Baráti László, Beleznay Soma, Csuma-Kovács Ádám, Czipó Bence, Hajnal Máté, Hopp Norbert, Kacz Dániel, Maga Balázs, Peszt Anna, Rábai Domonkos.
1 point:	28 students.
0 point:	11 students.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, April 2011