Problem B. 4354. (April 2011)

B. 4354. Given four distinct points A, B, C, D on the plane, construct two circles touching each other on the outside such that one of them passes through A and B, the other passes through C and D, and their point of tangency lies on the line segment BC.

(4 pont)

Deadline expired on May 10, 2011.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Az \(\displaystyle A\) és \(\displaystyle B\) pontokon átmenő kört jelölje \(\displaystyle k_1\), a másikat \(\displaystyle k_2\), a \(\displaystyle k_i\) kör középpontját \(\displaystyle O_i\), a két kör érintési pontját pedig \(\displaystyle E\).

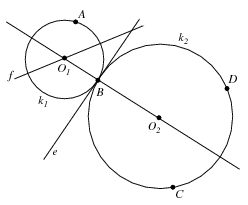
Először vizsgáljuk meg azt az esetet, amikor az \(\displaystyle E\) pont egybeesik a \(\displaystyle BC\) szakasz valamelyik végpontjával. Az \(\displaystyle E=B\) eset csak akkor fordulhat elő, ha a \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) pontok nem esnek egy egyenesre. Ekkor szerkesszük meg a \(\displaystyle k_2=BCD\) kört és annak \(\displaystyle O_2\) középpontját, továbbá a \(\displaystyle k_2\) kört \(\displaystyle B\)-ben érintő \(\displaystyle e\) egyenest. A feladatnak pontosan akkor lesz ilyen megoldása, ha az \(\displaystyle e\) egyenes elvásztja az \(\displaystyle A\) pontot a \(\displaystyle C,D\) pontoktól. Ha ez teljesül, akkor a megoldás egyértelmű lesz: az \(\displaystyle O_1\) pontot az \(\displaystyle O_2B\) egyenesnek és az \(\displaystyle AB\) szakasz \(\displaystyle f\) felező merőlegesének metszéspontjaként kapjuk meg. A \(\displaystyle E=C\) eset hasonlóképpen vizsgálható meg.

A továbbiakban azokat a megoldásokat keressük, ahol az \(\displaystyle E\) pont a \(\displaystyle BC\) szakasz belső pontja. Ha az \(\displaystyle A,D\) pontok közül valamelyik a \(\displaystyle BC\) egyenesre esik, akkor az egybe kell essen az \(\displaystyle E\) ponttal. Ez azt jelenti, hogy ha az \(\displaystyle A\), \(\displaystyle D\) pontok közül valamelyik a \(\displaystyle BC\) egyenesre esik, akkor csak az egyikük eshet arra, méghozzá a \(\displaystyle BC\) szakasz belső pontjaként. Tegyük fel, hogy \(\displaystyle A\) a \(\displaystyle BC\) szakasz belső pontja, de \(\displaystyle D\) nem esik a \(\displaystyle BC\) egyenesre. Ekkor a fenti eljárás szó szerint alkalmazható, ha abban felcseréljük az \(\displaystyle A\) és \(\displaystyle B\) pontok szerepét, es hasonlóképpen járhatunk el, ha a \(\displaystyle D\) pont a \(\displaystyle BC\) szakasz belső pontja, de \(\displaystyle A\) nem esik a \(\displaystyle BC\) egyenesre.

A továbbiakban tehát azt is feltesszük, hogy sem az \(\displaystyle A\), sem a \(\displaystyle D\) pont nem esik a \(\displaystyle BC\) egyenesre. Két esetet kell megkülönböztetnünk aszerint, hogy az \(\displaystyle A\), \(\displaystyle D\) pontok a \(\displaystyle BC\) egyenesnek ugyanarra az oldalára esnek, avagy nem.

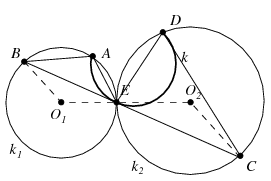
Mivel az \(\displaystyle E\) pont az \(\displaystyle O_1O_2\) szakasz belső pontja, a \(\displaystyle BO_1E\) és \(\displaystyle EO_2C\) irányított szögek egymást \(\displaystyle 360^\circ\)-ra egészítik ki. A kerületi szögek tétele alapján az első esetben ez azt jelenti, hogy az \(\displaystyle EAB\) és \(\displaystyle CDE\) szögek egymást \(\displaystyle 180^\circ\)-ra egészítik ki. Figyelembe véve, hogy az \(\displaystyle ABE\) és \(\displaystyle DEC\) háromszögek szögösszege, valamint a \(\displaystyle BEC\) egyenesszög nagysága is \(\displaystyle 180^\circ\), ez azt jelenti, hogy az \(\displaystyle AED\) irányított szög megegyezik az \(\displaystyle ABC\) és \(\displaystyle BCD\) irányított szögek összegével, ami kisebb kell legyen \(\displaystyle 180^\circ\)-nál, vagyis az \(\displaystyle E\) pont egy, az \(\displaystyle AD\) húr fölé szerkesztett \(\displaystyle k\) látóköríven helyezkedik el. Ez a feltétel könnyen láthatóan elégséges is, az \(\displaystyle E\) pont ismeretében pedig a két kör már könnyen megszerkeszthető.

Így 2, 1 vagy 0 megoldás adódik, annak megfelelően, hogy a \(\displaystyle k\) körívnek és a \(\displaystyle BC\) szakasznak hány közös belső pontja van.

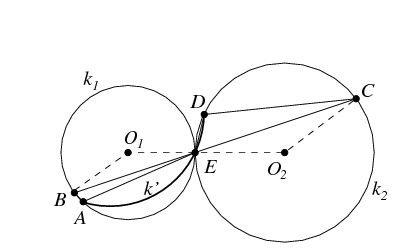
Végül vizsgáljuk azt az esetet, amikor a \(\displaystyle BC\) egyenes elválasztja az \(\displaystyle A\) és \(\displaystyle B\) pontokat. Az egyszerűség kedvéért tegyük fel, hogy \(\displaystyle CBA\angle\ge BCD\angle\). Ha itt egyenlőség áll, vagyis a \(\displaystyle BA\) és \(\displaystyle CD\) egyenesek párhuzamosak egymással, akkor világos, hogy a keresett \(\displaystyle E\) pont a \(\displaystyle BC\) és \(\displaystyle AD\) szakaszok metszéspontja lesz. Legyen tehát \(\displaystyle CBA\angle> BCD\angle\). Mivel ebben az esetben \(\displaystyle BAE\angle=CDE\angle\), azt kapjuk, hogy \(\displaystyle DEC\angle-AEB\angle=CBA\angle- BCD\angle\), vagyis

\(\displaystyle AED\angle=(180^\circ-DEC\angle)+AEB\angle=180^\circ-(CBA\angle- BCD\angle),\)

tehát az \(\displaystyle E\) pont ismétcsak egy, az \(\displaystyle AD\) húr fölé szerkesztett \(\displaystyle k'\) látóköríven helyezkedik el. Nem nehéz meggondolni, hogy a \(\displaystyle k'\) ívnek és a \(\displaystyle BC\) szakasznak pontosan egy közös belső pontja lesz, ami a keresett \(\displaystyle E\) pontot szolgáltatja.

Statistics:

15 students sent a solution.
4 points:	Kabos Eszter, Weimann Richárd.
3 points:	Bálint Csaba, Gyarmati Máté, Medek Ákos, Weisz Gellért.
2 points:	2 students.
1 point:	3 students.
0 point:	4 students.

Problems in Mathematics of KöMaL, April 2011