 Problem B. 4356. (April 2011)
Problem B. 4356. (April 2011)
B. 4356. On the same side of a given line segment AB, there are at most six similar triangles one side of which is AB. Prove that the third vertices of all these triangles are concyclic.
(4 pont)
Deadline expired on May 10, 2011.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az állítás triviális, ha a háromszög egyenlő szárú: szabályos háromszög esetén mind a hat háromszög egybeesik, ha pedig az egyenlő szárú háromszög nem szabályos, akkor három különböző háromszög keletkezik, melyek harmadik csúcsai nem esnek egy egyenesre.
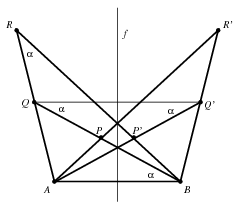
Ha a háromszög nem egyenlő szárú, akkor legyenek szögei \(\displaystyle \alpha<\beta<\gamma\). Az \(\displaystyle AB\) szakasz felező merőlegesét jelölje \(\displaystyle f\). A hat különböző csúcspont közül tekintsük azt a hármat, amelyik \(\displaystyle f\)-nek az \(\displaystyle A\) pontot tartalmazó oldalára esik; ezek az \(\displaystyle AB\) egyenestől való távolságuk növekvő sorrendjében legyenek \(\displaystyle P,Q,R\). A másik három pontot ezen pontok \(\displaystyle f\)-re vonatkozó tükörképeként kapjuk, ezeket jelölje rendre \(\displaystyle P',Q',R'\). Ekkor \(\displaystyle ABP\angle=ABQ\angle=\alpha\), \(\displaystyle ABR\angle=BAP\angle=\beta\) és \(\displaystyle BAQ\angle=BAR\angle=\gamma\). Ezek alapján
\(\displaystyle QRP'\angle=ARB\angle=\alpha=ABQ\angle=Q'QB\angle=Q'QP\angle=QQ'P'\angle,\)
vagyis a \(\displaystyle QP'\) szakasz az ugyanazon oldalára eső \(\displaystyle R\) és \(\displaystyle Q'\) pontokból azonos szög alatt látszik. Ez azt jelenti, hogy az \(\displaystyle R,Q,P',Q'\) pontok egy körre illeszkednek. Mivel ennek a körnek a középpontja \(\displaystyle f\)-re illeszkedik, a körvonal áthalad a \(\displaystyle P\) és az \(\displaystyle R'\) pontokon is.
Statistics:
48 students sent a solution. 4 points: Ágoston Péter, Bálint Csaba, Beleznay Soma, Boér Lehel, Bogár Blanka, Bősze Zsuzsanna, Csörgő András, Damásdi Gábor, Énekes Péter, Fatér Alexa, Fonyó Viktória, Forrás Bence, Gyarmati Máté, Győrfi 946 Mónika, Hajnal Máté, Herczeg József, Homonnay Bálint, Kabos Eszter, Kenéz Balázs, Máthé László, Medek Ákos, Molnár Ákos, Müller Dóra Tímea, Sagmeister Ádám, Schultz Vera Magdolna, Sieben Bertilla, Simig Dániel, Strenner Péter, Szabó 928 Attila, Varga 911 Szabolcs, Weimann Richárd, Weisz Ambrus, Weisz Gellért, Wiandt Zsófia, Zelena Réka, Zilahi Tamás, Zsakó András. 3 points: Barczel Nikolett, Csuma-Kovács Ádám, Nagy Róbert. 2 points: 6 students. 1 point: 1 student. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, April 2011
