 Problem B. 4366. (May 2011)
Problem B. 4366. (May 2011)
B. 4366. Let M denote the orthocentre of the acute-angled triangle ABC, and let A1, B1, C1, respectively, denote the circumcentres of triangles BCM, CAM, ABM. Prove that the lines AA1, BB1 és CC1 are concurrent.
(4 pont)
Deadline expired on June 10, 2011.
Sorry, the solution is available only in Hungarian. Google translation
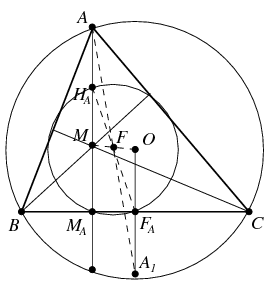
Megoldás. Az \(\displaystyle ABC\) háromszög Feuerbach-köre, melyet úgy kapunk, hogy a háromszög köré írható \(\displaystyle O\) középpontú \(\displaystyle k\) kört az \(\displaystyle M\) pontból felére kicsinyítjük, áthalad a \(\displaystyle BC\) oldal \(\displaystyle F_A\) felezőpontján, az \(\displaystyle AM\) szakasz \(\displaystyle H_A\) felezőpontján és az \(\displaystyle AM\) magasságvonal \(\displaystyle M_A\) talppontján. Mivel az \(\displaystyle F_AM_AH_A\) háromszög derékszögű, a Feuerbach-kör \(\displaystyle F\) középpontja, mely az \(\displaystyle OM\) szakasz felezőpontja, egybeesik az \(\displaystyle F_AH_A\) szakasz felezőpontjával, tehát az \(\displaystyle OF_A\) szakasz az \(\displaystyle MH_A\) szakasznak \(\displaystyle F\)-re vonatkozó tükörképe.
Ha az \(\displaystyle M\) pontot tükrözzük az \(\displaystyle M_A\) pontra, vagy ami ugyanazt jelenti, a \(\displaystyle BC\) egyenesre, a tükörkép a \(\displaystyle k\) körön van. Ebből következik, hogy a \(\displaystyle BMC\) háromszög köré írható kör a \(\displaystyle k\) körnek \(\displaystyle BC\) egyenesre vett tükörképe, tehát az \(\displaystyle A_1\) pont az \(\displaystyle O\) pontnak \(\displaystyle F_A\)-ra vett tükörképe. Így hát az is igaz, hogy az \(\displaystyle OA_1\) szakasz az \(\displaystyle MA\) szakasznak \(\displaystyle F\)-re vonatkozó tükörképe. Ez azt jelenti, hogy az \(\displaystyle AA_1\) szakasz felezőpontja éppen az \(\displaystyle F\) pont. Szimmetria okok miatt tehát az \(\displaystyle F\) pont az \(\displaystyle AA_{1}\), \(\displaystyle BB_{1}\) és \(\displaystyle CC_{1}\) szakaszok közös felezőpontja.
Statistics:
41 students sent a solution. 4 points: Antal Dóra, Baráti László, Bogár Blanka, Bősze Zsuzsanna, Damásdi Gábor, Fonyó Viktória, Frittmann Júlia, Gyarmati Máté, Győrfi 946 Mónika, Hajnal Máté, Herczeg József, Homonnay Bálint, Janzer Barnabás, Kaprinai Balázs, Maga Balázs, Máthé László, Medek Ákos, Mihálykó András, Nagy Róbert, Nemecskó István, Perjési Gábor, Sagmeister Ádám, Scharle Csilla, Schultz Vera Magdolna, Sieben Bertilla, Simig Dániel, Strenner Péter, Tekeli Tamás, Tossenberger Tamás, Tran Trong Hoang Tuan, Varga 911 Szabolcs, Weisz Gellért, Zahemszky Péter, Zelena Réka, Zilahi Tamás. 3 points: Dunay Luca, Lenger Dániel, Weimann Richárd. 2 points: 1 student. 0 point: 2 students.
Problems in Mathematics of KöMaL, May 2011
