 Problem B. 4370. (May 2011)
Problem B. 4370. (May 2011)
B. 4370. Let a, b, c denote the lengths of the sides of a triangle, and let u, v, w, respectively, be the distances of the centre of the incircle from the vertices opposite to the sides. Prove that .
(Suggested by J. Mészáros, Jóka)
(5 pont)
Deadline expired on June 10, 2011.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Ha \(\displaystyle a=b\), akkor nyilván \(\displaystyle u=v\), ha pedig \(\displaystyle a>b\), akkor \(\displaystyle u<v\). Ennek belátásához jelölje \(\displaystyle K\) a beírt kör középpontját, \(\displaystyle C_1\) a \(\displaystyle C\)-ből induló szögfelező talppontját, \(\displaystyle E_C\) pedig a beírt körnek az \(\displaystyle AB\) oldallal vett érintési pontját. A szögfelező-tétel szerint ekkor \(\displaystyle AC_1<BC_1\), továbbá\(\displaystyle \alpha>\beta\) miatt a \(\displaystyle CC_1A\) szög kisebb, mint a \(\displaystyle CC_1B\) szög, vagyis \(\displaystyle E_C\) az \(\displaystyle AC_1\) szakasz belső pontja. Ezért \(\displaystyle AE_C<AC_1<BC_1<BE_C\), és végül \(\displaystyle u=\sqrt{AE_C^2+KE_C^2}<\sqrt{BE_C^2+KE_C^2}=v\).
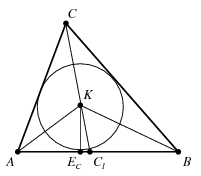
Legyen \(\displaystyle 1/u=a'\), \(\displaystyle 1/v=b'\), \(\displaystyle 1/w=c'\). Az általánosság megszorítása nélkül feltehetjük, hogy \(\displaystyle a\le b\le c\); ekkor a fentiek értelmében \(\displaystyle a'\le b'\le c'\). A rendezési tétel értelmében \(\displaystyle ab'+bc'+ca'\le aa'+bb'+cc'\) és \(\displaystyle ac'+ba'+cb'\le aa'+bb'+cc'\). A két egyenlőtlenség összeadásával nyert egyenlőtlenség mindkét oldalát az \(\displaystyle aa'+bb'+cc'\) mennyiséggel megnövelve kapjuk, hogy \(\displaystyle (a+b+c)(a'+b'+c')\le 3(aa'+bb'+cc')\), amit bizonyítanunk kellett. Ha azt is figyelembe vesszük, hogy \(\displaystyle a<b\) esetén \(\displaystyle a'<b'\), illetve \(\displaystyle b<c\) esetén \(\displaystyle b'<c'\), akkor könnyen megmutatható az is, hogy egyenlőség csakis az \(\displaystyle a=b=c\) esetben teljesülhet, vagyis ha szabályos háromszögről van szó.
Statistics:
21 students sent a solution. 5 points: Ágoston Péter, Baráti László, Bogár Blanka, Damásdi Gábor, Dinev Georgi, Dudás 002 Zsolt, Frittmann Júlia, Gyarmati Máté, Lenger Dániel, Maga Balázs, Nagy Róbert, Perjési Gábor, Schultz Vera Magdolna, Simig Dániel, Strenner Péter, Szabó 928 Attila, Szilágyi Gergely Bence, Tossenberger Tamás, Vajda Balázs, Zilahi Tamás. 4 points: Dolgos Tamás.
Problems in Mathematics of KöMaL, May 2011
