Problem B. 4377. (September 2011)

B. 4377. Regular triangles ABD, BCE, CAF are drawn to the sides of a triangle ABC on the outside. Let the midpoints of line segments DE, EF, FD be G, H, I, respectively. Prove that BG=CH=IA.

Suggested by Sz. Miklós, Herceghalom

(4 pont)

Deadline expired on October 10, 2011.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Az \(\displaystyle A,B,C\) pontoknak az \(\displaystyle I,G,H\) pontokra vett tükörképét jelölje rendre \(\displaystyle A',B',C'\), ekkor \(\displaystyle AA'=2IA\), \(\displaystyle BB'=2BG\) és \(\displaystyle CC'=2CH\). Szimmetria okok miatt elég lesz a \(\displaystyle BB'=CC'\) egyenlőséget igazolni.

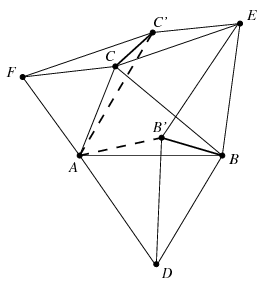
Az \(\displaystyle AD\) szakaszt az \(\displaystyle A\) pont körüli \(\displaystyle 60^\circ\)-os \(\displaystyle \Phi\) forgatás az \(\displaystyle AB\) szakaszba viszi. Mivel \(\displaystyle \overrightarrow{DB'}=\overrightarrow{BE}\) és az \(\displaystyle EBC\) szög is \(\displaystyle 60^\circ\)-os, ugyanez a forgatás a \(\displaystyle DB'\) szakaszt a \(\displaystyle BC\) szakaszba viszi, tehát az \(\displaystyle ADB'\) háromszöget az \(\displaystyle ABC\) háromszögbe viszi, és így \(\displaystyle \Phi(AB')=AC\). Ugyanígy \(\displaystyle \Phi(AC)=AF\) és \(\displaystyle \Phi(CB)=FC'\), vagyis \(\displaystyle \Phi(AB)=AC'\). Következésképpen \(\displaystyle \Phi(B'B)=CC'\), vagyis a \(\displaystyle \Phi\) forgatás a \(\displaystyle B'B\) szakaszt a \(\displaystyle CC'\) szakaszba viszi. Ezért a két szakasz valóban ugyanolyan hosszú.

Statistics:

64 students sent a solution.
4 points:	Ágoston Péter, Ágoston Tamás, Bánovics Gábor, Bingler Arnold, Bősze Zsuzsanna, Dinev Georgi, Fehér Zsombor, Fonyó Viktória, Forrás Bence, Gasparics Fanni, Halász Dániel, Kerti Dávid, Kocsis Laura, Leitereg András, Leitereg Miklós, Machó Bónis, Máthé László, Medek Ákos, Mester Márton, Nagy Anna Noémi, Nagy-György Pál, Nemes György, Papp Roland, Rábai Domonkos, Regele Balázs, Sagmeister Ádám, Schultz Vera Magdolna, Strenner Péter, Szabó 789 Barnabás, Szabó 928 Attila, Szekeres Ágnes, Szilágyi Gergely Bence, Tardos Jakab, Tekeli Tamás, Tossenberger Tamás, Varga 149 Imre Károly, Varga 911 Szabolcs, Varjú János, Varnyú József, Viharos Andor, Weimann Richárd, Zilahi Tamás, Zsakó András.
3 points:	9 students.
2 points:	3 students.
1 point:	2 students.
0 point:	7 students.

Problems in Mathematics of KöMaL, September 2011