Problem B. 4379. (September 2011)

B. 4379. Given the points different from the vertices where the exterior angle bisectors of a non-isosceles triangle intersect the circumscribed circle, construct the triangle.

(4 pont)

Deadline expired on October 10, 2011.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A háromszög csúcsait jelölje pozitív körüljárás szerint \(\displaystyle A,B,C\), a szóban forgó metszéspontokat értelemszerűen \(\displaystyle A',B',C'\), a körülírt kör középpontját \(\displaystyle O\).

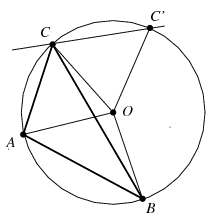
Minthogy a háromszög nem egyenlő szárú, \(\displaystyle C\ne C'\). A szokásos jelöléseket megtartva, dolgozzunk irányított szögekkel. Ha a \(\displaystyle C'\) pont az ábrán látható módon helyezkedik el, akkor \(\displaystyle BCC'\sphericalangle=90^\circ-\gamma/2\), ellenkező esetben \(\displaystyle BCC'\sphericalangle=270^\circ-\gamma/2\). A kerületi és középponti szögek között fennálló összefüggés alapján mindkét esetben \(\displaystyle BOC'\sphericalangle=180^\circ-\gamma\). Minthogy \(\displaystyle BOC\sphericalangle=2\alpha\), innen azt kapjuk, hogy \(\displaystyle C'OC\sphericalangle=BOC\sphericalangle-BOC'\sphericalangle=2\alpha+\gamma-180^\circ\). Hasonlóan \(\displaystyle COA'\sphericalangle=180^\circ-\alpha\), vagyis \(\displaystyle C'OA'\sphericalangle=C'OC\sphericalangle+COA'\sphericalangle=\alpha+\gamma= 180^\circ-\beta\). Ugyanilyen alapon \(\displaystyle A'OB'\sphericalangle=180^\circ-\gamma\) és \(\displaystyle B'OC'\sphericalangle=180^\circ-\alpha\).

Ennek alapján a szerkesztést a következőképpen végezhetjük el. Először is szükséges, hogy a három adott pont ne essen egy egyenesre. Ha ez teljesül, akkor a jól ismert módszerrel megszerkeszthetjük az \(\displaystyle O\) pontot és a háromszög köré írható kört. A három pontot jelöljük meg pozitív forgásirányban \(\displaystyle A',B',C'\) módon. Szükséges, hogy az \(\displaystyle A'OB', B'OC', C'OA'\) szögek \(\displaystyle 180^\circ\)-nál kisebbek legyenek, és semelyik kettő ne legyen egyenlő. Ha ez teljesül, akkor az ezeket \(\displaystyle 180^\circ\)-ra kiegészítő szögekkel megkapjuk a háromszög \(\displaystyle \gamma, \alpha, \beta\) szögeit. Ezután a \(\displaystyle C'O\) szakaszt \(\displaystyle O\) körül \(\displaystyle 2\alpha+\gamma-180^\circ\) szöggel elforgatva kapjuk meg a \(\displaystyle C\) pontot. Hasonló eljárással az \(\displaystyle A\) és \(\displaystyle B\) csúcsokat is megszerkeszthetjük. Könnyű meggondolni, hogy az említett feltételek teljesülése esetén az így kapott \(\displaystyle ABC\) háromszög lesz a feladat egyértelmű megoldása.

Statistics:

77 students sent a solution.
4 points:	Fehér Zsombor, Fonyó Viktória, Janzer Olivér, Machó Bónis, Mester Márton, Szabó 928 Attila.
3 points:	45 students.
2 points:	18 students.
1 point:	1 student.
0 point:	7 students.

Problems in Mathematics of KöMaL, September 2011