Problem B. 4380. (September 2011)

B. 4380. m points are chosen on the sides of a convex k-sided polygon, such that the resulting point set $\mathcal{P}$ of n=k+m elements is centrally symmetric. Prove that there may be at most 2n-3 line segments of equal length among the $\binom{n}{2}$ line segments determined by the points of the set $\mathcal{P}$ . For what point sets $\mathcal{P}$ are there 2n-3 line segments of equal length?

(5 pont)

Deadline expired on October 10, 2011.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Nyilván $\displaystyle n\ge 4$ páros szám. Ha $\displaystyle n=4$, akkor $\displaystyle k=4$, $\displaystyle m=0$, a konvex $\displaystyle k$-szög egy paralelogramma, az állítás pedig nyilvánvaló: nem lehet minden oldal és mindkét átló ugyanolyan hosszú. Az is világos, hogy pontosan akkor lesz 5 ugyanolyan hosszú szakasz, ha a sokszög olyan rombusz, melynek egyik szöge $\displaystyle 60^\circ$-os.

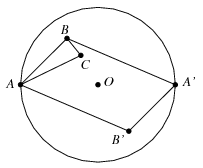
Most tegyük fel, hogy $\displaystyle n\ge 6$, és az állítást $\displaystyle (n-2)$-elemű ponthalmazok esetén már beláttuk. A szimmetriaközéppontot jelölje $\displaystyle O$, a $\displaystyle \mathcal{P}$ ponthalmaznak $\displaystyle O$-tól egyik legtávolabb eső pontja legyen $\displaystyle A$, ennek tükörképe $\displaystyle O$-ra $\displaystyle A'$. Ekkor $\displaystyle A'\in \mathcal{P}$, és a ponthalmaz összes pontja az $\displaystyle AA'$ átmérőjű körlemezen helyezkedik el. Legyen $\displaystyle d>0$ egy tetszőleges távolság. Azt állítjuk, hogy az $\displaystyle AA'$ egyenesre támaszkodó bármely zárt $\displaystyle H$ félsíkban a $\displaystyle \mathcal{P}$ ponthalmaznak legfeljebb egy olyan pontja található, amely az $\displaystyle A$ ponttól $\displaystyle d$ távolságra helyezkedik el. Tegyük fel ugyanis, hogy $\displaystyle B,C\in \mathcal{P}\cap H$ és $\displaystyle AB=AC=d$. Az általánosság megszorítása nélkül felthető, hogy $\displaystyle CAO\sphericalangle<BAO\sphericalangle$. Nyilván $\displaystyle d<AA'$. Mivel az $\displaystyle ABC$ háromszög egyenlőszárú, $\displaystyle ABC\sphericalangle<90^\circ\le ABA'\sphericalangle$. Ezért a $\displaystyle C$ pont vagy az $\displaystyle ABA'$ háromszög belsejében, vagy az $\displaystyle AA'$ szakasz belsejében helyezkedik el, tehát mindenképpen az $\displaystyle ABA'B'$ paralelogramma belsejében, ahol $\displaystyle B'$ a $\displaystyle B$ pontnak $\displaystyle O$-ra vonatkozó tükörképe. Ez viszont ellentmond a $\displaystyle \mathcal{P}$ ponthalmaz konstrukciójának, hiszen $\displaystyle B'\in \mathcal{P}$.

A $\displaystyle \mathcal{P}$ ponthalmaznak tehát legfeljebb két olyan pontja van, amely $\displaystyle d$ távolságra van $\displaystyle A$-tól. A szimmetria miatt ez $\displaystyle A$ helyett az $\displaystyle A'$ pontra is igaz. Hagyjuk el most a ponthalmazból az $\displaystyle A$ és $\displaystyle A'$ pontokat. Így egy olyan $\displaystyle \mathcal{P}'$ ponthalmazt kapunk, amelynek $\displaystyle n-2\ge 4$ pontja van, és ugyanúgy szimmetrikus az $\displaystyle O$ pontra. Könnyű látni, hogy ez is csak a feladatban leírt módon jöhetett létre. Az indukciós feltevés miatt a $\displaystyle \mathcal{P}'$ pontjai által meghatározott szakaszok között legfeljebb $\displaystyle 2(n-2)-3=2n-7$ lehet $\displaystyle d$ hosszúságú, így a $\displaystyle \mathcal{P}$ pontjai által meghatározott szakaszok között valóban legfeljebb $\displaystyle (2n-7)+4=2n-3$ lehet $\displaystyle d$ hosszúságú.

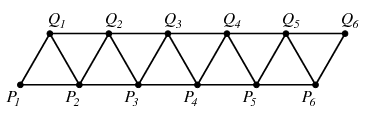
Most megmutatjuk, hogy $\displaystyle 2n-3$ darab $\displaystyle d$ hosszúságú szakasz akkor és csak akkor található, ha $\displaystyle k=4$, $\displaystyle m$ páros, a $\displaystyle k$-szög egy olyan paralelogramma, melynek egyik oldala $\displaystyle d$, másik $\displaystyle (\frac{m}{2}+1)d$ hosszú, az egyik szöge $\displaystyle 60^\circ$-os, és az $\displaystyle m$ pont úgy helyezkedik el a két hosszabbik oldalon, hogy azokat $\displaystyle d$ hosszúságú részekre osztja. Más szóval, ha a ponthalmaz $\displaystyle P_1,\ldots,P_{m/2+2},Q_1,\ldots,Q_{m/2+2}$ alakú, ahol $\displaystyle \overrightarrow{P_1P_2}=\overrightarrow{P_2P_3}=\ldots=\overrightarrow{P_{m/2+1}P_{m/2+2}}= \overrightarrow{Q_1Q_2}=\overrightarrow{Q_2Q_3}=\ldots=\overrightarrow{Q_{m/2+1}Q_{m/2+2}}$ és $\displaystyle \overrightarrow{P_1Q_1}$ $\displaystyle d$ hosszúságú vektorok, ahol $\displaystyle P_2P_1Q_1\sphericalangle=60^\circ$. Ebben a ponthalmazban a $\displaystyle d$ hosszú szakaszok éppen a $\displaystyle P_iP_{i+1}$, $\displaystyle Q_iQ_{i+1}$, $\displaystyle P_iQ_i$ és $\displaystyle Q_iP_{i+1}$ szakaszok, melyek száma

$\displaystyle \left(\frac{m}{2}+1\right)+\left(\frac{m}{2}+1\right)+ \left(\frac{m}{2}+2\right)+\left(\frac{m}{2}+1\right)=2m+5=2n-3.$

Ezt $\displaystyle n=4$ esetén már beláttuk, az általános eset pedig könnyen igazolható indukcióval. Ehhez egyrészt azt kell észrevennünk, hogy ha az $\displaystyle n\ge 6$ pontú $\displaystyle \mathcal{P}$ ponthalmazban $\displaystyle 2n-3$ darab $\displaystyle d$ hosszú szakasz van, akkor a fenti érveléssel kapott $\displaystyle \mathcal{P}$ ponthalmazban $\displaystyle 2(n-2)-3$ darab $\displaystyle d$ hosszú szakasznak kell lenni, ami az indukciós feltevés szerint $\displaystyle \mathcal{P}'$ szerkezetét már meghatározza, másrészt, hogy az elhagyott $\displaystyle A,A'$ pontokból 2-2 $\displaystyle d$ hosszúságú szakasznak kell indulni, ami az $\displaystyle A,A'$ pontok helyzetét az $\displaystyle n=6$ esettől eltekintve egyértelműen meghatározza, az $\displaystyle n=6$ esetben pedig két megoldást enged meg, melyek azonban egybevágóak. A részleteket az olvasóra bízzuk.

Statistics:

5 students sent a solution.

5 points: Mester Márton, Strenner Péter.

4 points: Katona Dániel, Nagy Róbert.

0 point: 1 student.

Problems in Mathematics of KöMaL, September 2011

5 students sent a solution.
5 points:	Mester Márton, Strenner Péter.
4 points:	Katona Dániel, Nagy Róbert.
0 point:	1 student.

Already signed up?
New to KöMaL?