 Problem B. 4387. (October 2011)
Problem B. 4387. (October 2011)
B. 4387. In the cyclic hexagon ABCDEF, AB=BC, CD=DE and EF=FA. Prove that the area of the triangle BDF is half the area of the hexagon.
(4 pont)
Deadline expired on November 10, 2011.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Először is nem árt meggondolni, hogy a körülírt kör középpontja a sokszög belsejébe esik, ellenkező esetben ugyanis a sokszöget a kör középpontjától elválasztó oldalánál az összes többi oldal rövidebb lenne. Legyen a kör sugara egységnyi, középpontja legyen \(\displaystyle O\), az \(\displaystyle AB\), \(\displaystyle CD\) és \(\displaystyle EF\) oldalakhoz tartozó középponti szögeket pedig jelölje rendre \(\displaystyle \alpha\), \(\displaystyle \beta\), illetve \(\displaystyle \gamma\), ekkor \(\displaystyle \alpha+\beta+\gamma=180^\circ\).
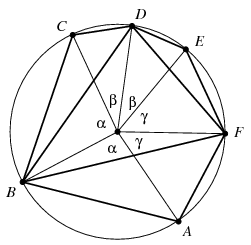
Az \(\displaystyle AOB\) és \(\displaystyle BOC\) háromszögek területe például ekkor \(\displaystyle (\sin \alpha)/{2}\). A hatszöget az \(\displaystyle O\) pontból hat háromszögre felbontva kapjuk, hogy a hatszög területe
\(\displaystyle T=\sin \alpha+\sin\beta+\sin\gamma\ .\)
Hasonlóképpen a \(\displaystyle BOD\) háromszög területe
\(\displaystyle \frac{\sin(\alpha+\beta)}{2}=\frac{\sin\gamma}{2}\ ,\)
hiszen \(\displaystyle \gamma=180^\circ-(\alpha+\beta)\). A \(\displaystyle BDF\) háromszöget az \(\displaystyle O\) pontból három háromszögre felbontva kapjuk, hogy a \(\displaystyle BDF\) háromszög területe
\(\displaystyle t=t_{BOD}+t_{DOF}+t_{FOB}=\frac{\sin\gamma}{2}+\frac{\sin\alpha}{2}+ \frac{\sin\beta}{2}=\frac{T}{2}\ .\)
Statistics:
150 students sent a solution. 4 points: 75 students. 3 points: 41 students. 2 points: 21 students. 1 point: 8 students. 0 point: 2 students. Unfair, not evaluated: 3 solutionss.
Problems in Mathematics of KöMaL, October 2011
