 Problem B. 4389. (October 2011)
Problem B. 4389. (October 2011)
B. 4389. Given four points A, B, C and D on a line in this order, consider all pairs of touching circles such that one circle passes through A and B and the other passes through C and D. Determine the locus of the points of contact.
(4 pont)
Deadline expired on November 10, 2011.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Tekintsünk egy ilyen érintő körpárt. Az érintési pontot jelölje \(\displaystyle E\), ez nyilván nem eshet az adott egyenesre. Az \(\displaystyle E\) pontban a két kör kívülről érinti egymást. Ebben a pontban húzott közös érintőjük az egyenest a \(\displaystyle BC\) szakasz belsejében metszi, ezt a metszéspontot jelölje \(\displaystyle O\). Erre az \(\displaystyle O\) pontra fennáll, hogy \(\displaystyle OA\cdot OB=OE^2=OC\cdot OD\).
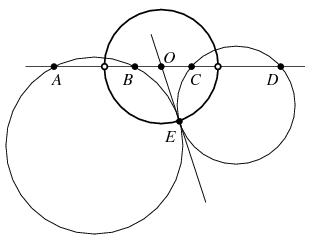
Nem nehéz kiszámolni, hogy az \(\displaystyle OA\cdot OB=OC\cdot OD\) feltételnek eleget tevő \(\displaystyle O\) pont a \(\displaystyle BC\) szakaszt \(\displaystyle BD:AC\) arányban osztja, vagyis az érintő körpár helyzetétől függetlenül
\(\displaystyle OB=\frac{BC\cdot BD}{AC+BD},\quad OB=\frac{BC\cdot AC}{AC+BD}.\)
Ekkor \(\displaystyle BC\cdot BD+AB\cdot(AC+BD)=AB\cdot AC+AC\cdot BD=AC\cdot AD\) miatt
\(\displaystyle OB\cdot OA=\frac{BC\cdot BD}{AC+BD}\cdot \left(\frac{BC\cdot BD}{AC+BD}+AB\right)= \frac{AC\cdot AD\cdot BC\cdot BD}{(AC+BD)^2},\)
vagyis az \(\displaystyle E\) pont az \(\displaystyle O\) középpontú,
\(\displaystyle r=\frac{\sqrt{AC\cdot AD\cdot BC\cdot BD}}{AC+BD}\)
sugarú körvonalon helyezkedik el. Ennek a körvonalnak az adott egyenesre nem illeszkedő pontjai pedig valamennyien a mértani helyhez tartoznak, hiszen egy ilyen \(\displaystyle E\) pontra \(\displaystyle OA\cdot OB=OE^2=OC\cdot OD\) miatt teljesül, hogy az \(\displaystyle OE\) egyenes az \(\displaystyle ABE\) és a \(\displaystyle CDE\) kört is érinti, így e két kör valóban az \(\displaystyle E\) pontban érinti egymást.
Statistics:
39 students sent a solution. 4 points: Ágoston Péter, Ágoston Tamás, Barna István, Dinev Georgi, Fehér Zsombor, Gyarmati Máté, Győrfi 946 Mónika, Havasi 0 Márton, Homonnay Bálint, Janzer Olivér, Maga Balázs, Máthé László, Mester Márton, Ódor Gergely, Strenner Péter, Tossenberger Tamás. 3 points: Beleznay Soma, Bősze Zsuzsanna, Kalló Kristóf, Katona Dániel, Kecskés Boglárka, Medek Ákos, Nagy Róbert, Németh Gergely, Öreg Botond, Schultz Vera Magdolna, Szilágyi Gergely Bence, Tekeli Tamás, Weimann Richárd, Zilahi Tamás. 2 points: 3 students. 1 point: 2 students. 0 point: 4 students.
Problems in Mathematics of KöMaL, October 2011
