Problem B. 4408. (December 2011)

B. 4408. In a triangle ABC, the lengths of sides AC and BC are fixed, and the angle at vertex C is variable. The midpoint of side AC is M, the midpoint of side BC is N, and the centre of the square drawn over the side AB on the outside is O. For what value of $ACB\sphericalangle$ will the sum of the distances OM and ON be a maximum?

(4 pont)

Deadline expired on February 10, 2012.

Sorry, the solution is available only in Hungarian. Google translation

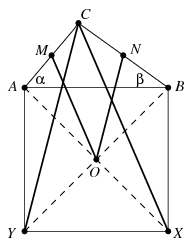
Megoldás. A négyzet másik két csúcsát $\displaystyle X$ és $\displaystyle Y$ jelöli az ábra szerint, akkor az $\displaystyle OM$ szakasz az $\displaystyle AXC$, $\displaystyle ON$ pedig a $\displaystyle BYC$ háromszög középvonala, tehát $\displaystyle OM+ON=(XC+YC)/2$, vagyis az $\displaystyle XC+YC$ összeget szeretnénk maximalizálni. A szokásos jelölésekkel a $\displaystyle BXC$ háromszögre a koszinusz-tételt felírva kapjuk, hogy

$\displaystyle CX^2=a^2+c^2-2ac\cos(\beta+90^\circ)= a^2+c^2+2ac\sin\beta=a^2+c^2+2ab\sin\gamma,$

hiszen a szinusz-tétel szerint $\displaystyle c\sin\beta=b\sin\gamma$.

Ugyanígy $\displaystyle CY^2=b^2+c^2+2ab\sin\gamma$. Lévén $\displaystyle c^2=a^2+b^2-2ab\cos\gamma$,

$\displaystyle XC+YC=\sqrt{2a^2+b^2+2ab(\sin\gamma-\cos\gamma)}+ \sqrt{a^2+2b^2+2ab(\sin\gamma-\cos\gamma)}.$

Világos, hogy ez a kifejezés akkor veszi fel a maximumát, ha $\displaystyle \sin\gamma-\cos\gamma$ értéke a lehető legnagyobb. Minthogy

$\displaystyle \sin\gamma-\cos\gamma=\sqrt{2}\sin(\gamma-45^\circ),$

ez nyilván $\displaystyle \gamma=135^\circ$ esetén következik be.

Statistics:

29 students sent a solution.

4 points: Bingler Arnold, Czipó Bence, Fehér Zsombor, Fonyó Viktória, Janzer Olivér, Jávorszky Natasa, Kaprinai Balázs, Kiss 902 Melinda Flóra, Lucskai Gábor, Machó Bónis, Mester Márton, Mihálykó András, Ódor Gergely, Sticza Gergő, Strenner Péter, Szabó 928 Attila, Weimann Richárd.

3 points: Árkos Gergely, Nagy-György Pál, Schultz Vera Magdolna, Somogyvári Kristóf, Szilágyi Gergely Bence.

2 points: 4 students.

1 point: 1 student.

0 point: 2 students.

Problems in Mathematics of KöMaL, December 2011

29 students sent a solution.
4 points:	Bingler Arnold, Czipó Bence, Fehér Zsombor, Fonyó Viktória, Janzer Olivér, Jávorszky Natasa, Kaprinai Balázs, Kiss 902 Melinda Flóra, Lucskai Gábor, Machó Bónis, Mester Márton, Mihálykó András, Ódor Gergely, Sticza Gergő, Strenner Péter, Szabó 928 Attila, Weimann Richárd.
3 points:	Árkos Gergely, Nagy-György Pál, Schultz Vera Magdolna, Somogyvári Kristóf, Szilágyi Gergely Bence.
2 points:	4 students.
1 point:	1 student.
0 point:	2 students.

Already signed up?
New to KöMaL?