Problem B. 4415. (January 2012)

B. 4415. Let B be an interior point of a line segment AC. The Thales circles of the line segments AB, BC and AC are k₁, k₂ and k₃, respectively, with radii of r₁, r₂ and r₃. A common exterior tangent of circles k₁ and k₂ cuts the circle k₃ into two circular segments. The radius of the circle inscribed in the smaller circular segment is r₄. Prove that r₁^.r₂=r₃^.r₄.

(Suggested by Sz. Miklós, Herceghalom)

(4 pont)

Deadline expired on February 10, 2012.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Egy helyesbítéssel kell kezdenünk: a feladat pontatlanul lett kitüzve. Az adott körszeletbe ugyanis végtelen sok különböző érintő kör írható. A megoldás során, mint ahogy azt a legtöbb megoldó is tette, hallgatólagosan feltételezzük, hogy a lehető legnagyobb ilyen körről van szó, melyet \(\displaystyle k_4\)-gyel jelölünk.

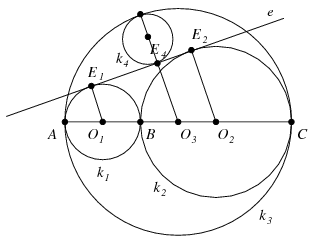
Jelölje a \(\displaystyle k_i\) kör középpontját \(\displaystyle O_i\), a szóban forgó érintőt \(\displaystyle e\), és \(\displaystyle E_i\) azt a pontot, amelyben az \(\displaystyle e\) egyenes a \(\displaystyle k_i\) kört érinti. Mivel \(\displaystyle O_1O_3+r_1=O_2O_3+r_2=r_3=r_1+r_2\), \(\displaystyle O_1O_3=r_2\) és \(\displaystyle O_2O_3=r_1\). Az \(\displaystyle O_1E_1\), \(\displaystyle O_2E_2\), \(\displaystyle O_3E_4\) szakaszok merőlegesek az \(\displaystyle e\) egyenesre, tehát egymással párhuzamosak. Ezért \(\displaystyle E_1E_4:E_4E_2=O_1O_3:O_3O_2=r_2:r_1\).

Ennélfogva a sík tetszőleges \(\displaystyle P\) pontjára felírható

\(\displaystyle \overrightarrow{PO_3}=\frac{r_1\overrightarrow{PO_1}+r_2\overrightarrow{PO_2}}{r_1+r_2}\quad \hbox{és} \quad \overrightarrow{PE_4}=\frac{r_1\overrightarrow{PE_1}+r_2\overrightarrow{PE_2}}{r_1+r_2},\)

ahonnan

\(\displaystyle \overrightarrow{O_3E_4}=\frac{r_1\overrightarrow{O_1E_1}+r_2\overrightarrow{O_2E_2}}{r_1+r_2},\)

vagyis

\(\displaystyle r_3-2r_4={O_3E_4}=\frac{r_1^2+r_2^2}{r_1+r_2}.\)

Innen \(\displaystyle r_1+r_2=r_3\) miatt

\(\displaystyle r_3(r_3-2r_4)=r_1^2+r_2^2=r_3^2-2r_1r_2\)

adódik, ami rendezés és 2-vel való leosztás után a bizonyítandó állításra vezet.

Statistics:

74 students sent a solution.
4 points:	Balogh Tamás, Barna István, Bingler Arnold, Bősze Zsuzsanna, Csigi Máté, Csuma-Kovács Rita, Di Giovanni Márk, Dinev Georgi, Emri Tamás, Englert Franciska, Fatér Alexa, Fehér Zsombor, Fonyó Viktória, Forrás Bence, Herczeg József, Homonnay Bálint, Janzer Barnabás, Janzer Olivér, Jávorszky Natasa, Jenei Adrienn, Juhász 214 Dániel, Kabos Eszter, Kacz Dániel, Khayounti Sára, Kiss 902 Melinda Flóra, Leitereg Miklós, Maga Balázs, Makk László, Medek Ákos, Mester Márton, Mócsy Miklós, Nagy Anna Noémi, Nagy Róbert, Nagy-György Pál, Sagmeister Ádám, Schultz Vera Magdolna, Schwarcz Tamás, Somogyvári Kristóf, Strenner Péter, Szabó 789 Barnabás, Szabó 928 Attila, Szilágyi Gergely Bence, Varnyú József, Viharos Andor, Weimann Richárd, Zilahi Tamás.
3 points:	23 students.
2 points:	2 students.
1 point:	3 students.

Problems in Mathematics of KöMaL, January 2012