 Problem B. 4420. (January 2012)
Problem B. 4420. (January 2012)
B. 4420. The lengths of the edges of a cuboid are 7, 14 and 21 units. Which pair of skew face diagonals lying on adjacent faces have the smallest distance?
(Based on a Kavics Kupa problem, 2011)
(4 pont)
Deadline expired on February 10, 2012.
Sorry, the solution is available only in Hungarian. Google translation
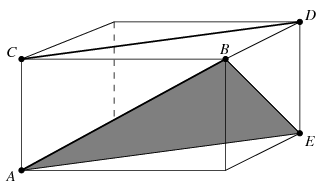
Megoldás. Tekintsük az \(\displaystyle AB\) és \(\displaystyle CD\) lapátlókat az ábra szerint (ez nem méretarányos, az élek hossza lényegtelen). Az \(\displaystyle ABCD\) tetraéder \(\displaystyle V'\) térfogata a téglatest \(\displaystyle V\) térfogatának egyhatod része. A tetraéder térfogata nem változik, ha annak \(\displaystyle D\) csúcsát az \(\displaystyle ABC\) lapsíkkal párhuzamosan az \(\displaystyle E\) pontba eltoljuk. Az \(\displaystyle ABCE\) tetraéder térfogatát viszont megkapjuk úgy, ha az \(\displaystyle ABE\) háromszög \(\displaystyle T\) területét megszorozzuk az ehhez tartozó \(\displaystyle m\) magassággal, majd az eredményt elosztjuk 3-mal. Innen a két lapátló távolságára \(\displaystyle m=V/3T\) adódik. Mivel az \(\displaystyle ABE\) háromszöget a téglatest három különböző hosszú lapátlója határolja, vagyis egybevágóság erejéig a téglatest által egyértelmüen meghatározott, a fenti képletben \(\displaystyle V\) és \(\displaystyle T\) értéke is egyértelmüen meg van határozva a téglatest éleinek hossza által. Ennélfogva a szóban forgó távolság a lapátlók választásától függetlenül mindig ugyanakkora.
Statistics:
34 students sent a solution. 4 points: Ágoston Tamás, Bingler Arnold, Böszörményi Borbála, Csigi Máté, Fehér Zsombor, Fonyó Viktória, Havasi 0 Márton, Herczeg József, Homonnay Bálint, Janzer Olivér, Kabos Eszter, Katona Dániel, Maga Balázs, Medek Ákos, Mester Márton, Nagy Bence Kristóf, Németh Gergely, Sagmeister Ádám, Schwarcz Tamás, Strenner Péter, Szabó 789 Barnabás, Szabó 928 Attila, Szász Dániel Soma, Tossenberger Tamás, Weimann Richárd, Zilahi Tamás. 2 points: 1 student. 1 point: 4 students. 0 point: 3 students.
Problems in Mathematics of KöMaL, January 2012
